












adolfodarriba@
observatoriolascasqueras.es



Se dice de Galileo, que no fue capaz de convencer a sus contemporáneos de que la Tierra era redonda y giraba. Como se sabe, fue Foucault a mediados del siglo XIX, más de dos siglos después de Galileo, que demostró públicamente que la Tierra rotaba. Suspendió un péndulo bajo la cúpula del Panteón de París, utilizando un cable de 67 metros de largo y una esfera de 28 kg. El plano de oscilación del péndulo debería permanecer invariable en el espacio si no interviniesen fuerzas externas, pero como la Tierra gira sobre su propio eje, todos los presentes comprendieron que el movimiento lateral era provocado por la rotación de la Tierra, ya que el momento inercial se conserva.
La casualidad o la mala fortuna, según como se mire, tuve que trabajar en la estación de Chamartín (Madrid) en una empresa de paquetería. En mi trabajo llevaba por los mismos andenes una carretilla que era capaz de tirar enganchados unos 10 carros o más. Muy parecido a los carros que transportan las maletas en los aeropuertos.
Cuando me asignaron una carretilla ya me dijeron que tenía que circular por los andenes por la izquierda, para evitar que se cayeran los carros a la vía. Personalmente, probé la veracidad de este hecho experimentalmente en más de una ocasión teniendo mis compañeros razón, con la consiguiente reprimenda de mis jefes, maquinistas, inspectores de circulación y demás. Realmente, si circulaba por la derecha se caían a la vía.
Recuerdo aún que les preguntaba a mis compañeros por qué sucedía esto. Todos me dijeron lo más intuitivo. ¡Los andenes están inclinados hacia la derecha! ¡Están mal construidos! Y claro, y yo pensaba, ¿cómo una estación ferroviaria con más de 12 andenes y con una longitud de unos 400 metros o más cada uno, todos ellos iban a estar mal construidos y hacia el mismo lado?
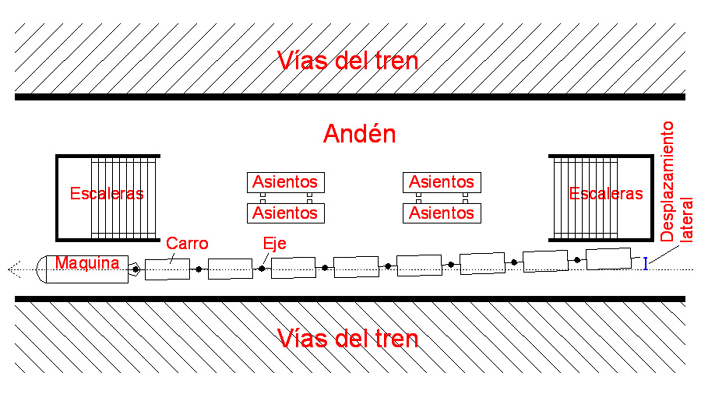
En días de lluvia, me cercioré de que los andenes vertían agua correctamente, la mitad del andén hacia un lado y la otra mitad, hacia el otro. Es decir, estaban correctamente construidos. Entonces, ¿por qué había que circular por la izquierda en los andenes?
Leyendo libros científicos en aquellos años, hacia 1.993, me tropecé con la fuerza de Coriolis. Siempre se ha puesto el ejemplo de que al quitar el tapón de un lavabo lleno de agua, rota en la entrada al sumidero en sentido contrario de las agujas del reloj en el hemisferio Norte, y en el hemisferio Sur al contrario. Este mito es absurdo, ya que el movimiento aleatorio del agua y el rozamiento desigual del lavabo es muy superior a la fuerza de Coriolis. Es como hacer girar el océano con el movimiento de la mano.
Los efectos de la rotación de la Tierra son de gran importancia en el estudio de los sistemas de vientos, de las corrientes marítimas y de los lanzamientos de cohetes.
Colón como marinero lo conocía perfectamente, aunque no sabía el por qué. Sabía que para llegar a las "Américas" de la manera más fácil, había que ir primero a Canarias, para que la corriente marítima le empujara hacia allí y para volver, hacia España, empujándole la misma corriente marítima.
Aunque parezca la misma ley física, la fuerza de Coriolis y el movimiento giratorio del péndulo, tienen sus grandes diferencias. De acuerdo que se produce por el movimiento giratorio de la Tierra sobre su eje, pero mientras que la fuerza de Coriolis es acumulativa, el movimiento giratorio del péndulo es siempre constante. Por ejemplo, la parte derecha de los raíles de los trenes en el hemisferio Norte están más desgastados, causados por los vagones que lleva la máquina al hacer efecto "látigo". Sólo en teoría, porque en la práctica es totalmente inobservable por la gran resistencia al desgaste de los raíles (lo he verificado personalmente después de llevar más de 13 años en contratas ferroviarias). Además, estoy asumiendo que los trenes tienen dos carriles, una para cada sentido. Es decir, estoy suponiendo que los trenes circulan siempre en el mismo sentido sobre los mismos raíles.
Lo que al principio es una pequeña fuerza en los primeros vagones, se convierte en un gran desplazamiento lateral al final de los vagones o en el anterior ejemplo, en los carros, por lo que la fuerza de Coriolis es acumulativa. El movimiento giratorio del péndulo sólo depende de la latitud del observador y no de lo largo o grande que sea el péndulo.
De hecho, la fuerza de Coriolis es tan intensa que fijaba el número total de carros que podíamos transportar, porque aunque circulases por la izquierda para evitar que se cayeran a la vía, los últimos carros no solo rozaban los pilares de la escalera, si no que se llegaban a incrustar consiguiendo detener totalmente la carretilla.
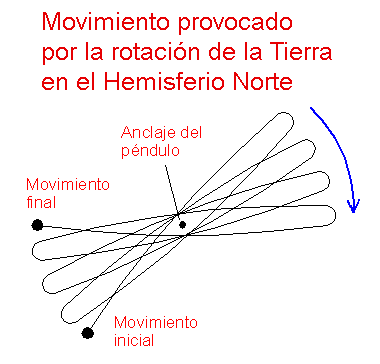
Otro ejemplo sería que la parte derecha de la orilla de un río está mucho más erosionado, tanto lateralmente como en profundidad que el lado izquierdo, por lo general. Por el contrario, el giro lateral del péndulo es constante al igual que el movimiento diurno de la tierra, porque el momento inercial se conserva (bien lo saben los ingenieros de los satélites artificiales cuando instalan los giroscopios para no perder las coordenadas de referencia en el espacio).
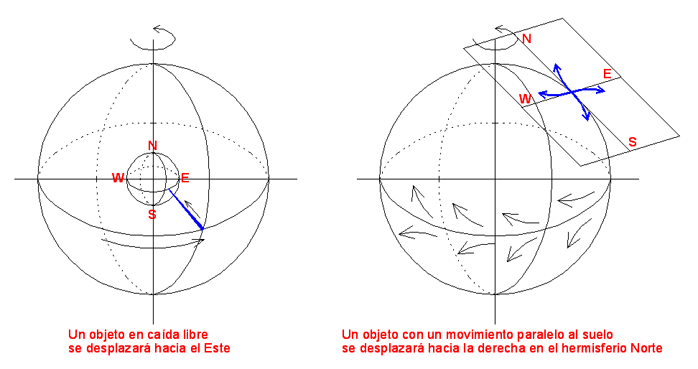
Tengo aquí que aclarar que la forma e intensidad de la fuerza de Coriolis depende de si el objeto en movimiento está en caída libre o paralelo al suelo. Si está en caída libre, el objeto en movimiento se desplazará hacia el Este siendo nula en los polos y máxima en el ecuador al ser perpendicular al eje terrestre. Por el contrario, si el movimiento es paralelo al suelo, es decir, perpendicular al anterior movimiento o caída libre, entonces los objetos en movimiento se desplazarán hacia la derecha en el hemisferio Norte y en el hemisferio Sur hacia la izquierda, siendo nula en los polos y en el ecuador, aunque aumentando de intensidad hacia el ecuador ya que estamos cada vez más lejos del eje terrestre. Lo que sucede es que se hace nulo en el ecuador por estar el objeto en movimiento en un plano paralelo al eje terrestre.
Es decir, la fuerza de Coriolis provoca un desplazamiento lateral provocado por el movimiento giratorio de la Tierra sobre su eje. Entonces siguiendo este mismo razonamiento, la Tierra tiene otro movimiento giratorio más débil: El movimiento de Translación alrededor del Sol. Existen otros movimientos más débiles en nuestro planeta, como la Libración de la Luna, que hace zarandear a nuestro planeta o el de Precesión de los Equinoccios. Pero centrémonos en el movimiento de Translación.
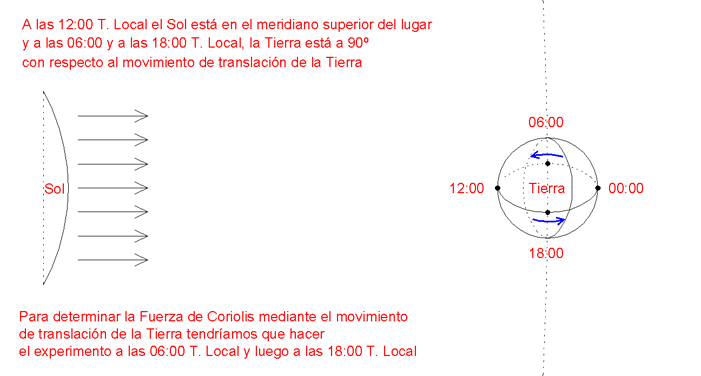
Como nos enseñó Sir Issac Newton, considerado como el mayor científico de todos los tiempos, la Tierra gira alrededor del Sol gracias a la fuerza gravitatoria, provocando un movimiento giratorio. Entonces, si hacemos el mismo experimento con los carros para detectar la fuerza de Coriolis al amanecer y luego 12 horas más tarde, en uno se añadiría este pequeño efecto y en el otro experimento se restaría. Dicho valor experimental sería el doble que éste pequeño efecto, como lo es también el paralaje anua de una estrella.
De aquí se desprende que este efecto es independiente de la latitud, siendo 365 veces más débil con respecto al lugar donde realicemos el experimento, aunque el experimento lo desarrollemos en cualquier lugar del planeta.
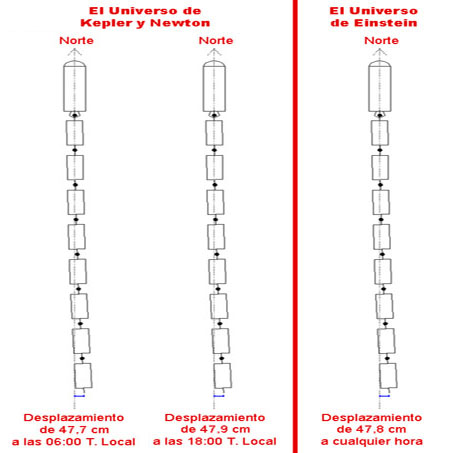
Es decir, para poder conseguir una medida experimental de 2 milímetros que estaría justo dentro de nuestras posibilidades de medición, (un milímetro hacia la izquierda y 12 horas más tarde, otro milímetro hacia la derecha), necesitaríamos que la fuerza de Coriolis provocase una desviación lateral de nuestros carros de 366 milímetros a las 06:00 Tiempo Local y 364 milímetros a las 18:00 Tiempo Local, siempre y cuando nuestro lugar del experimento esté situado en latitudes cercanas al Ecuador, donde la fuerza de Coriolis es máxima en éste caso.
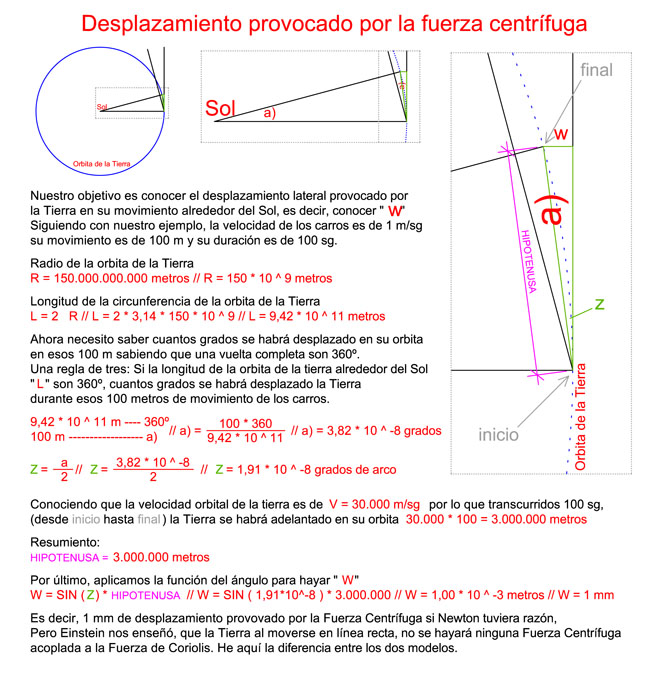
Esto sería verdad si Newton tuviese razón, pero Einstein nos enseñó que la Tierra se mueve en línea recta sobre un universo cuatridimensional. Que a nosotros nos parezca que la Tierra gira alrededor del Sol en curva, es porque somos seres de tres dimensiones y observamos el universo en esas mismas dimensiones.
¿Qué quiero decir con esto? Que el débil efecto que quería hallar en el anterior experimento por el movimiento de translación de la Tierra sería inexistente, porque como he dicho antes, la Tierra se mueve en línea recta alrededor del Sol, y este concepto es extensible a todos los demás movimientos menores que tiene la Tierra, porque siempre se desplazará por el universo por su propia inercia en línea recta, en un universo cuatridimensional.
Iba a obtener el mismo resultado negativo que el experimento de Michelson y Morley para conocer la velocidad de la Tierra a través del "éter", y es cuando apareció Einstein para explicarnos que la velocidad de la luz es independiente de la velocidad del observador.
Ahora es cuando de una manera muy sutil y delicada, podremos averiguar la veracidad de la teoría de la relatividad general.
Desde siempre se nos han puesto los tres típicos ejemplos a favor de esta teoría, que son: El avance del perihelio de la órbita de Mercurio, la desviación de la luz de las estrellas cerca de un campo gravitatorio y el retraso de los relojes. Últimamente tenemos otras pruebas a su favor, por ejemplo los cuasar dobles, las lentes gravitacionales, el enrojecimiento de las enanas blancas o de las estrellas de neutrones, la pérdida de energía en un sistema compacto muy estrecho causando un lento alejamiento entre ambas con la consiguiente disminución de la velocidad orbital, etc.
Está claro que estas observaciones y experimentos no están al alcance de cualquiera. Se necesitan los más grandes telescopios del mundo para comprobar la veracidad de la teoría. El experimento que acabo de redactar si que se podría averiguar con los medios cotidianos de que disponemos. La fuerza de Coriolis es tan intensa al ser una fuerza acumulativa, que aunque realicemos el experimento con unos carros de muy poca calidad con las ruedas locas se aprecia perfectamente ya que tiene un desplazamiento lateral muy considerable (casi tanto como los carritos de los supermercados).
De hecho, fue una pena no poder cuantificar el desplazamiento lateral en aquellos años porque necesitaba realizar unas cuantas mediciones para luego hacer la media y otras tantas, 12 horas más tarde con los mismos carros. Creo que mi jefe no lo entendería y además delante de todos los pasajeros.
El problema de estos experimentos, es que como Einstein tiene razón, en nuestras medidas serán iguales dentro de los errores de precisión que podamos cometer. No debemos achacarlos a la poca precisión, si no que la Tierra se mueve en línea recta alrededor del Sol, a través del espacio-tiempo, en un universo cuatridimensional. Una bella y fácil forma de comprobar la veracidad de la teoría de la relatividad general sin tener que recurrir a los grandes observatorios o a los experimentos desarrollados con el mayor grado de precisión.
Entiendo que os preguntéis, ¿cómo es posible comprobar la teoría de la relatividad general con un experimento tan simple y rudimentario en las mediciones? Pues hay dos opciones: Que a nadie se le ha ocurrido o algo falla en mi tesis. De momento, no observo ningún error.
Sinceramente, agradecería vuestras críticas.
Conclusiones:
1º) Aquí estoy demostrando dos experimentos que corrobora la rotación de la Tierra: El péndulo de Foucault y el desplazamiento lateral provocado por la fuerza de Coriolis. Si Galileo se hubiera cerciorado de alguno de estos dos experimentos, descubiertos siglos más tarde, no le hubieran condenado por blasfemar. Resultaría muy complicado para sus contemporáneos, haber puesto otro tipo de argumento que no fuera la rotación de la Tierra.
2º) En el universo de Kepler y Newton, los planetas giran alrededor del Sol en curva, incluso se aceleran cuando pasan por el perihelio. En el universo de Einstein, los planetas tienen un movimiento inercial uniforme y se mueven en línea recta alrededor del Sol. Que nos parezca que giran alrededor del Sol y se aceleren es motivo que somos seres de tres dimensiones, pero la realidad es que los planetas tienen un movimiento inercial uniforme y en línea recta. La gran diferencia entre estos dos modelos, es que en el universo de Kepler y Newton, la Tierra tendría una fuerza centrífuga acoplada constantemente a la fuerza de Coriolis porque se movería en círculos alrededor del Sol, pero en el universo de Einstein, no existiría ninguna fuerza centrifuga acoplada a la fuerza de Coriolis ya que la Tierra se mueve en línea recta.
3º) Como la Tierra se mueve en línea recta en el universo de Einstein, la fuerza de Coriolis provoca un desplazamiento lateral, solo y exclusivamente causado por la rotación de la Tierra sobre su eje. De todos los movimientos menores que puede tener la Tierra y balanceos que causan los demás planetas a su paso, la Tierra se moverá siempre en línea recta a través del espacio-tiempo curvo. No es la Tierra la que se balancea y cambia de rumbo. Es el tejido espacio-tiempo el que se deforma para que la Tierra vaya siempre en línea recta.
4º) También estoy exponiendo un experimento que jamás se ha realizado más allá de la demostración de la rotación de la Tierra sobre su eje. Es necesario una mayor precisión para alcanzar el modelo teórico aquí descrito y no podemos desechar la demostración práctica, simplemente porque sepamos en qué tipo de universo vivimos. En el universo de Kepler y Newton, o en el universo de Einstein. Es decir, si vivimos en un universo de tres o de cuatro dimensiones, y si realmente la fuerza de la gravedad curva el espacio-tiempo.
5º) Incluso cuando un objeto o una simple partícula, se aproxima a un agujero negro cerca de la velocidad de la luz y lo bordea, cerca del horizonte de sucesos, en el universo de Kepler y Newton, pensaríamos que el objeto sufriría una fuerza centrífuga brutal cerca del perihelio, incluso se despedazaría. Pero en el universo de Einstein, como el objeto tiene un movimiento inercial uniforme y sobre todo en línea recta, despreciando las demás fuerzas, aun cuando su velocidad es cercana a la velocidad de la luz, dicho objeto no sentiría ninguna diferencia. Pensaríamos que el objeto está en una parte tranquila del universo. (Si el objeto es despedazado, no es por la fuerza centrífuga, sino por la fuerza de marea). Es decir, si realizara un experimento a bordo para captar la fuerza centrífuga, no la hallaría. De hecho, un argumento equivocado es que la radiación sincrotrónica es causada por la alta velocidad de las partículas cerca de los cuásar. La causa verdadera es que los cuásar emiten radiación sincrotrónica porque el intenso campo magnético desvía la trayectoria de los electrones de su movimiento natural de línea recta, al ser desviados. La radiación térmica es producida por la fricción de las partículas.
6º) Siguiendo con el mismo argumento que el apartado anterior, si llevásemos a bordo un laser y un giroscopio y los hiciéramos apuntar hacia adelante, es decir, en la dirección de nuestro movimiento hacia el agujero negro, cuando pasáramos cerca del perihelio tanto el laser como el giroscopio variaría en la misma cantidad de movimiento que nosotros que los llevamos a bordo, apuntando siempre hacia adelante, pero las estrellas de fondo ya no las tendríamos delante, si no que estarían girando hacia un lado. Es decir, sería el universo entero el que girase hacia un lado. En este punto se rompe cualquier sistema de referencia relativo.
7º) La fórmula matemática de la fuerza de Coriolis es diferente a la que aquí expongo, ya que no quiero conocer cuál es la cantidad de fuerza generada, sino cuánto es el desplazamiento lateral que provoca la fuerza de Coriolis. Por eso, en la fórmula clásica de la fuerza de Coriolis viene implícita la masa. Para conocer la desviación lateral no influye en absoluto. Es decir, la cantidad de desplazamiento lateral provocado por la fuerza de Coriolis, no depende de la masa.
Resumiendo:
Este estudio viene a decir básicamente que mediante un experimento relativamente sencillo, se puede saber si vivimos en un universo de tres o de cuatro dimensiones.
La diferencia fundamental está si la Tierra se mueve alrededor del Sol en curva (provocado por la fuerza gravitatoria) en un universo de tres dimensiones o se mueve en línea recta (en el tejido espacio-tiempo) en un universo de cuatro dimensiones.
Lo que está claro, es que la fuerza centrífuga solo se hallaría acoplado en los cuerpos en movimiento si la Tierra gira alrededor del Sol en curva (Universo de Newton), y no en línea recta (Universo de Einstein).
Es decir, la rotación de la Tierra provoca la fuerza de Coriolis y el movimiento de la Tierra alrededor del Sol, provoca la fuerza centrífuga solo en un universo de tres dimensiones. He aquí donde radica la diferencia para conocer si vivimos en un universo de tres o de cuatro dimensiones. Si los cuerpos experimentan o no esta fuerza centrífuga.
Nota: de una simple observación de la naturaleza, lo que hago es llevarlo a su máxima expresión, e incluso llevarlo al absurdo, para ver la veracidad de mi teoría.





|

|