adolfodarriba@ observatoriolascasqueras.es

Detection of the time delays in AGNs In this study, I will mainly focus on finding a behavior pattern common to all AGNs. Each AAVSO light curve corresponds to 1,000 days. Although I show the three types of explosions, as I have defined it in my previous article (it is the first link of this Web), Type III Explosions are the most energetic. Therefore, they are the ones that best adjust to secondary explosions. As their behavior are the least random, it is easier to find a pattern of behavior among them all. As seen in the following light curves of the AAVSO, in most of them there is a time delay in the AGNs studied. The maximum brightness in the optician is the point that I consider as the Main Explosion, marked as 0 days. It is also observed that the maximum brightness in Gamma rays usually occurs about 3 days before. The time delay in all subclasses of AGNs (Blazars, Quasars, Seyfert 2 galaxies, etc.) is the same. The only thing that is appreciable in its curves of light, is its lower light amplitude. What is more difficult for me is to detect the exact moment of the main explosion and secondary explosions. As I gather more light curves, I will attach it and reduce the errors. That is, I want to further define the light curve and its time delay. In the graph below, a light curve of an Explosion of Type III is theoretically represented, with a maximum brightness very marked in the 85 days, as bright as the main explosion. If the AGN were really a Type I Explosion, secondary explosions would not be detected in most cases. If it were an Explosion of Type II, the maximums in the secondary explosions would be more representative, but it would not have a maximum in the 85 days.

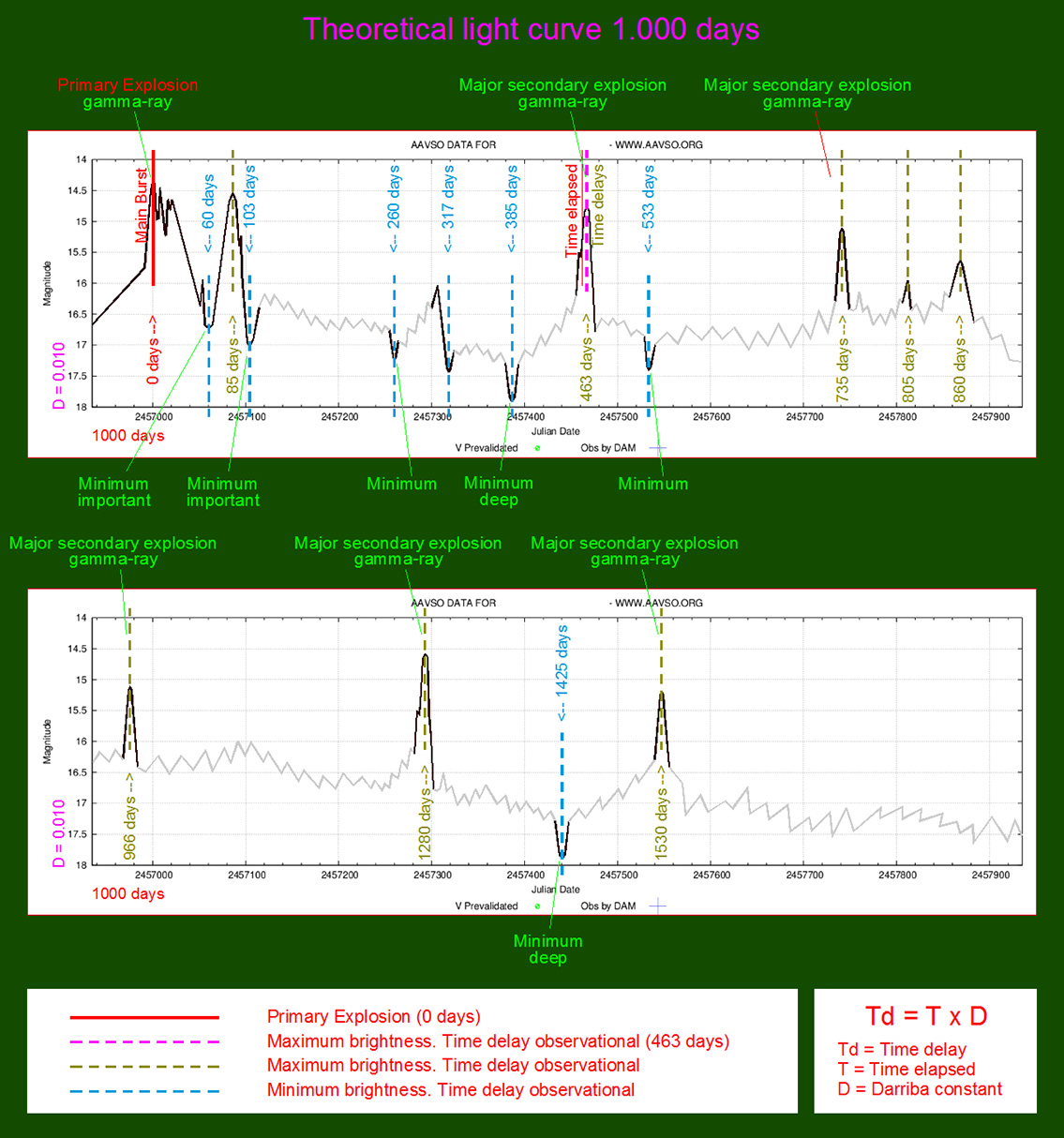
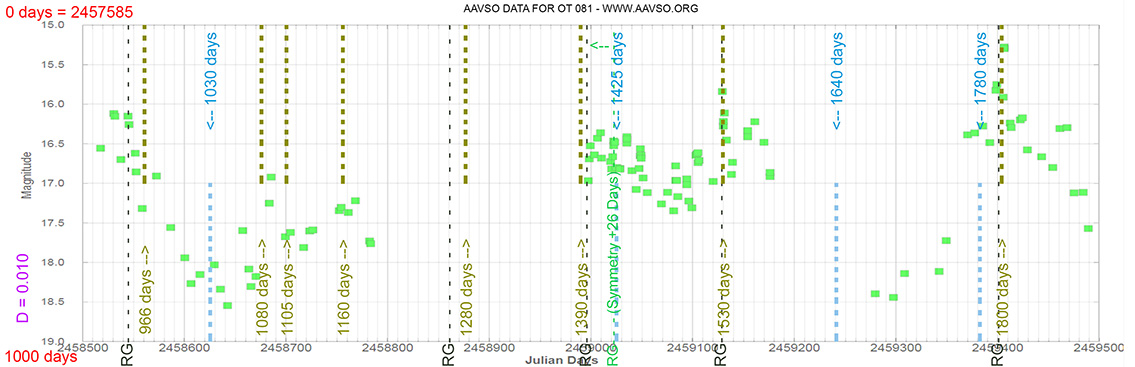
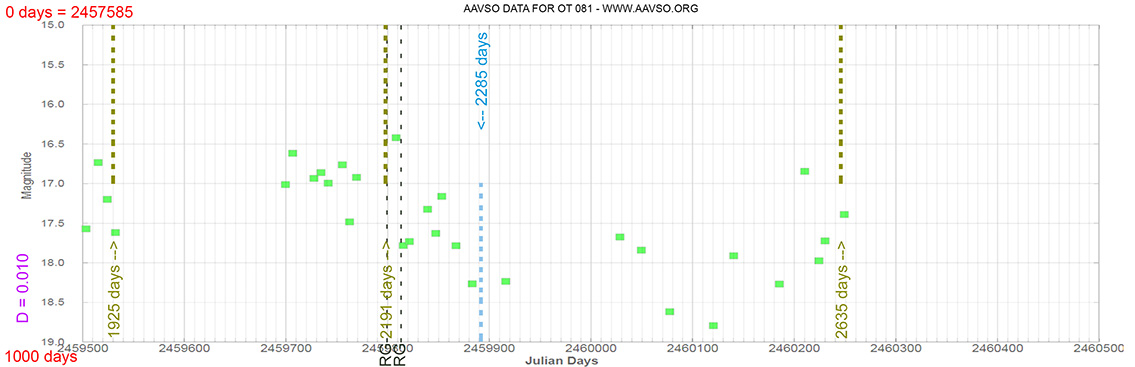
Basic concepts - The Blazares are still predictable. Light curves 1,000 days. - There are three types of main explosions. Type I, Type II and Type III. - At the time of a principal explosion, a cascade of stable elements is produced as radioactive. - The radioactive decays of the different elements cause secondary explosions. - Depending on the sharpness of the secondary explosions, the width of the jet can be known. - As radioactive elements behave like well-defined atomic clocks, when a delay occurs in secondary explosions, it is a clear indication of their time delay. That is, each Blazar has its own time delay. Types of main explosions - Those of Type I, usually move near their minimum brightness, without large variations occurring when they reach their secondary explosions, although sometimes there is some significant increase. Its most important feature is that no explosions are detected between 60 and 100 days. Its trajectory is usually flat or even descending slightly. - Those of type II, have a greater movement within the light curve, detecting an increase in brightness at 75 and 90 days later. - Those of type III, are the most energetic explosions. A secondary explosion is detected at 85 days, almost as bright as the main one. They are the most predictable. Its movement within the light curve is similar to those of Type II. 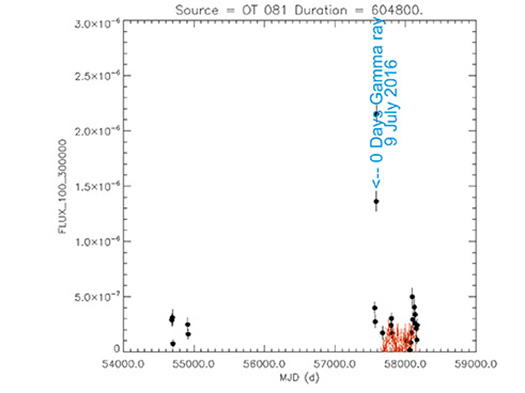Concept in Gamma flashes - In Gamma rays, the main explosion usually happens about 3 to 10 days before the optic. - In secondary explosions usually occurs with the same time delay as the optical or about 6 days later. - Occasionally, a Gamma flash is observed three or four weeks apart from the previous, which would correspond to a maximum of light in the optic. - This symmetry is produced because the two lobes are connected and we would be seeing the Gamma flash coming from the opposite lobe. That is, we would see a symmetry in the Gamma flash, not being the same in their detection, although physically they would be the same. - The time taken from the first Gamma flash to the second is the distance that the two lobes are separated. It is not strictly correct because space-time is dragged and this greatly influences this appreciation. - It is possible that the symmetry is produced by the precession of the two emitting lobes, when rotating. Hence, the symmetry of each blazar never occurs in a certain exact time. 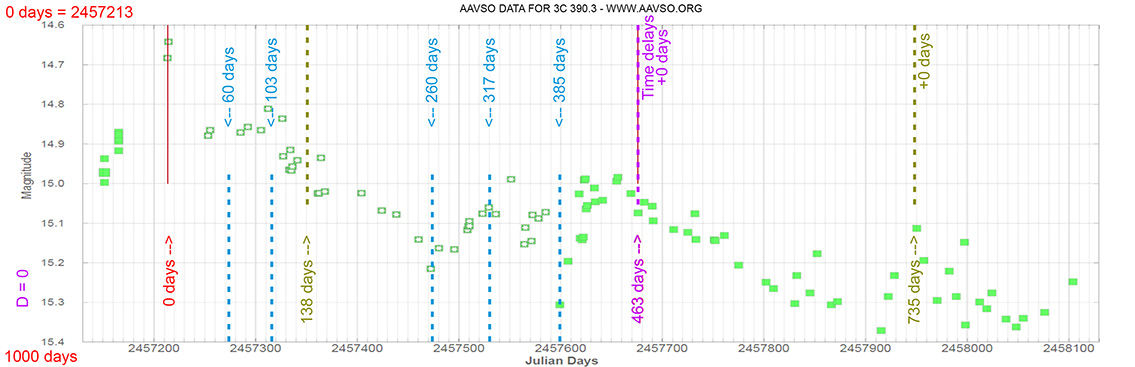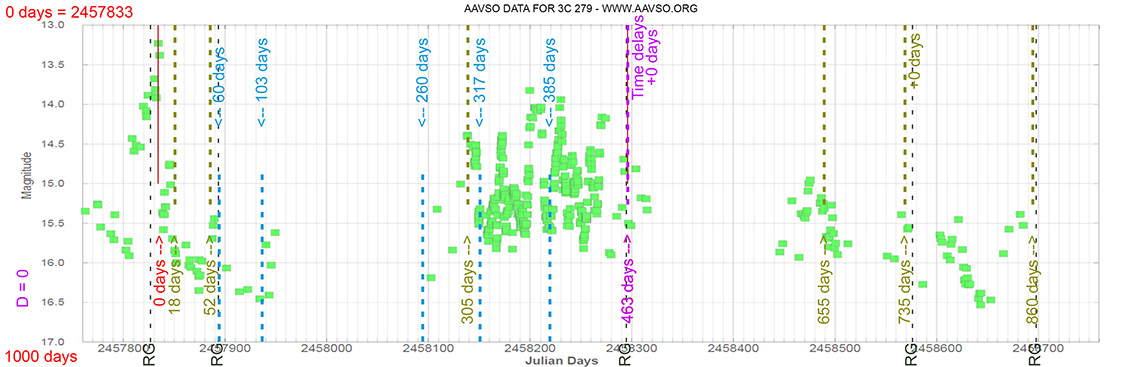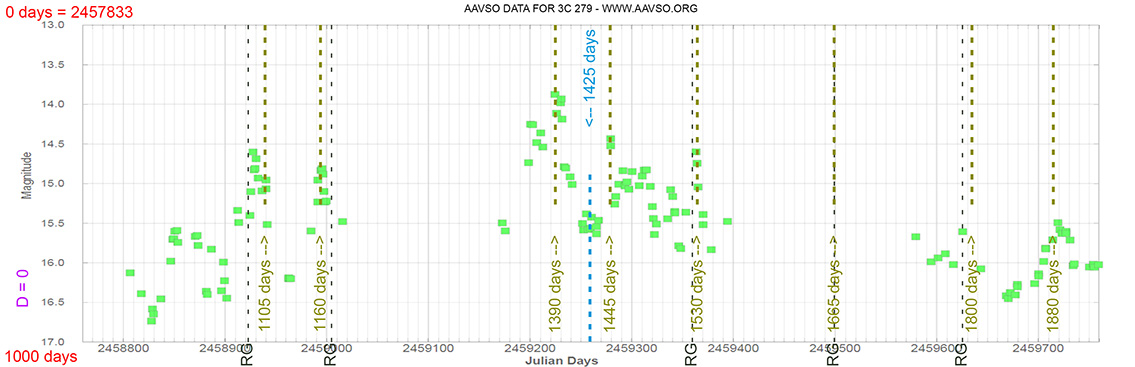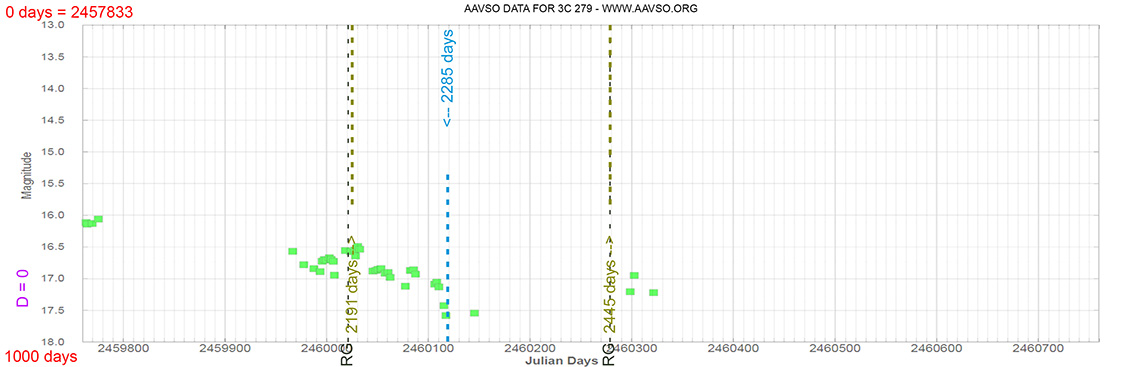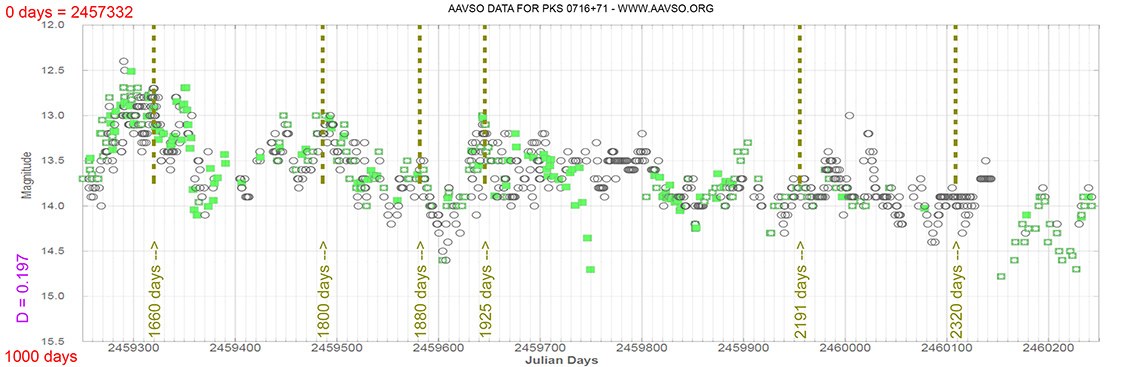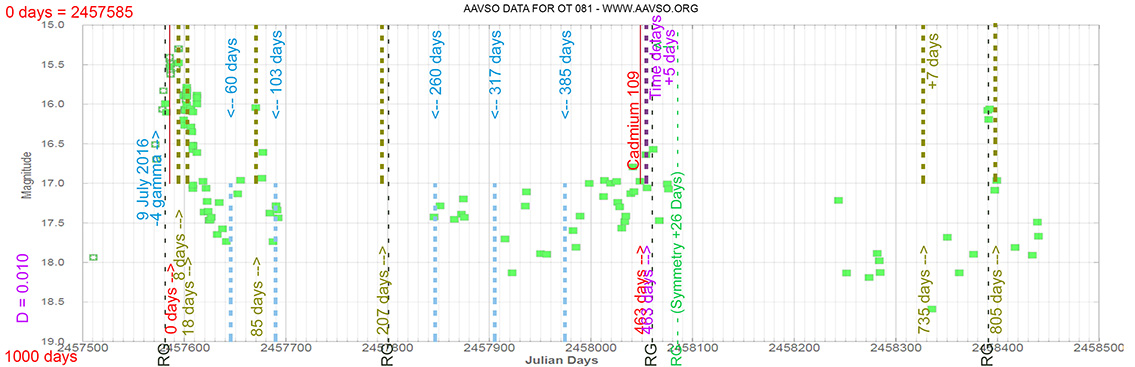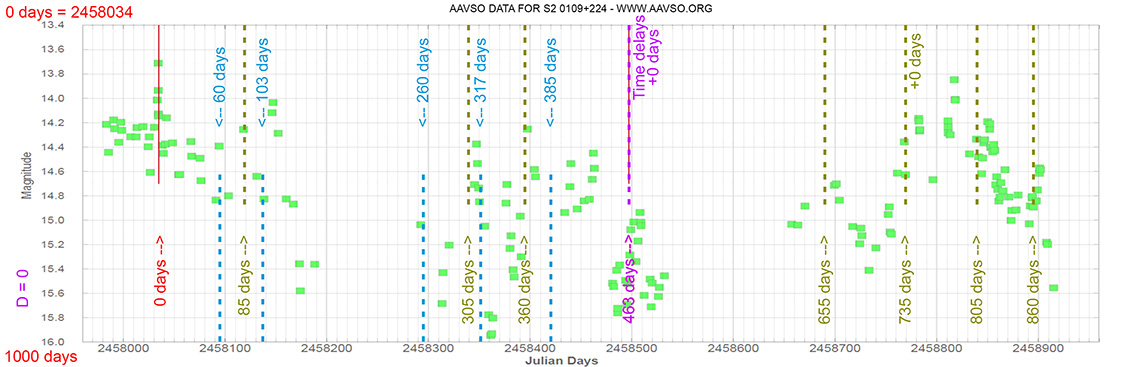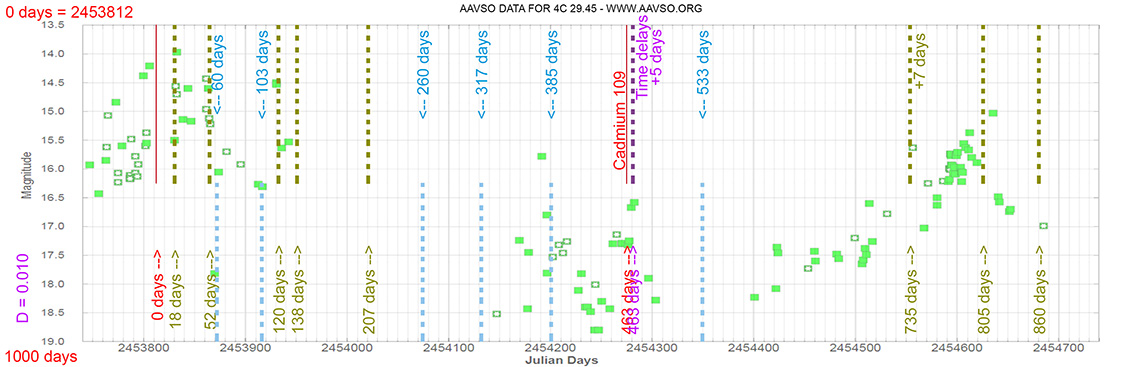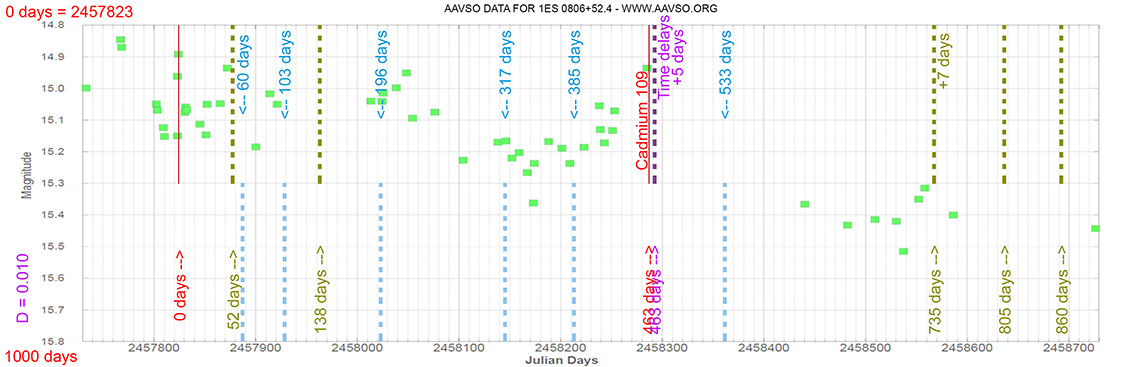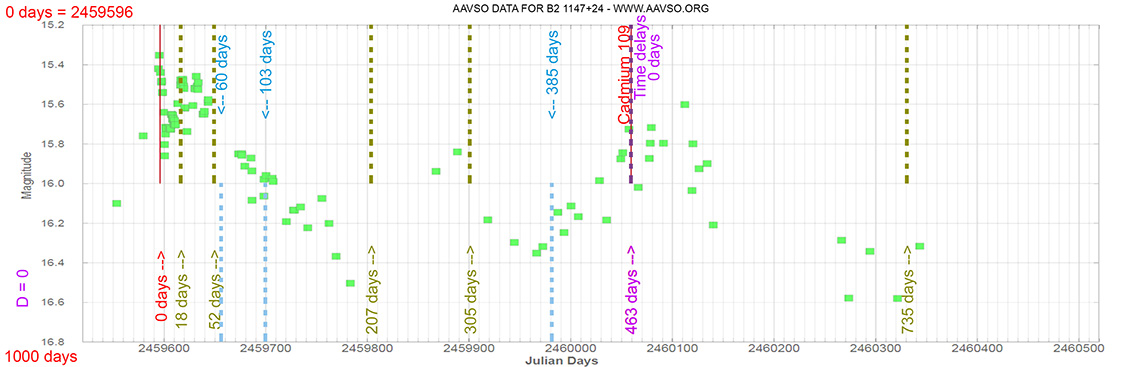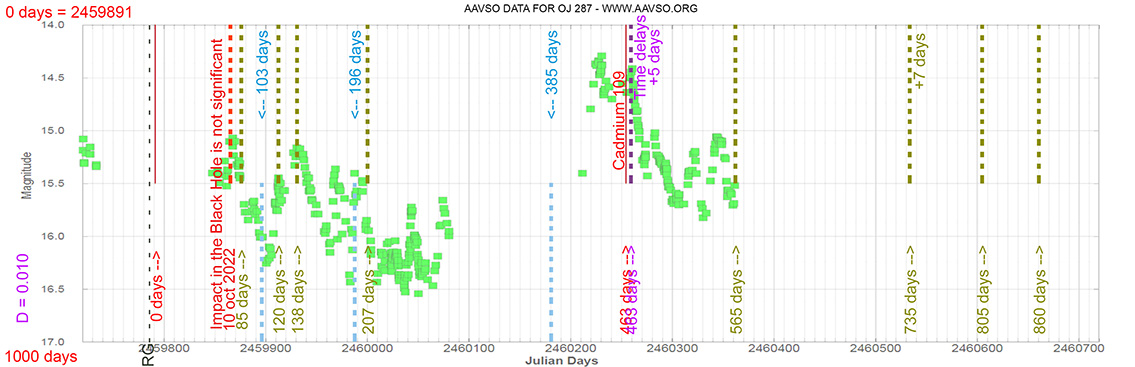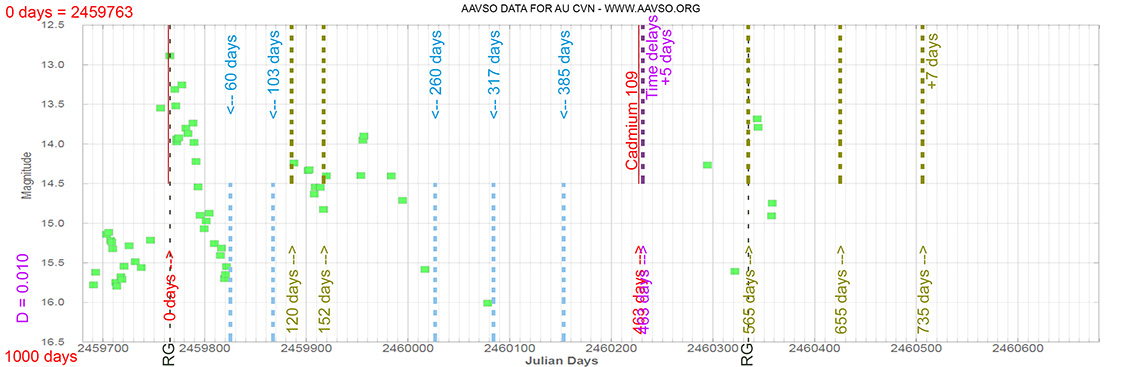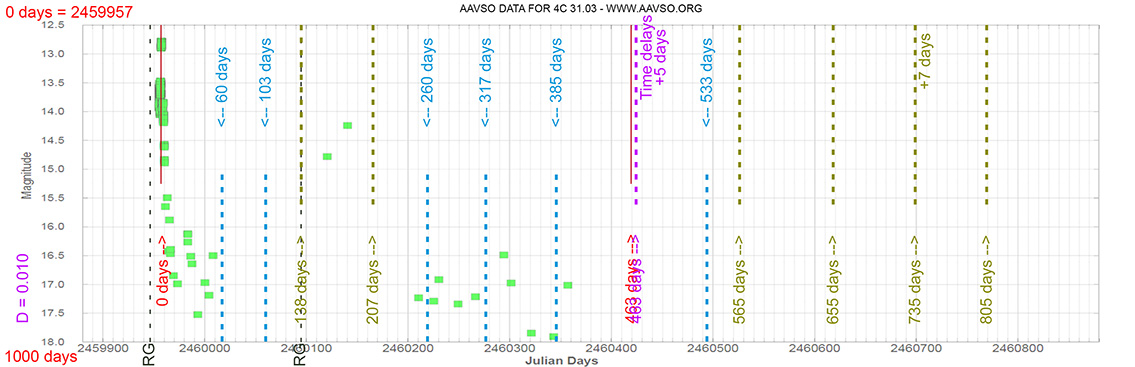Mathematic expression Each Blazar has its own time delay, so I apply a constant (D). In my theoretical model above, the constant could be: D = 0.010 That is, when the maximum brightness occurs at 463 days (T), its time delay corresponds (Td): Td = T x D // Td = 463 x 0.010 // Td = 5 Days (The maximum would occur 5 days later) and when it reaches 735 days (T), it corresponds to: Td = T x D // Td = 735 x 0.010 // Td = 7 Days (The maximum would occur 7 days later) As can be seen, the time delay (Td) is proportional to the elapsed time (T). 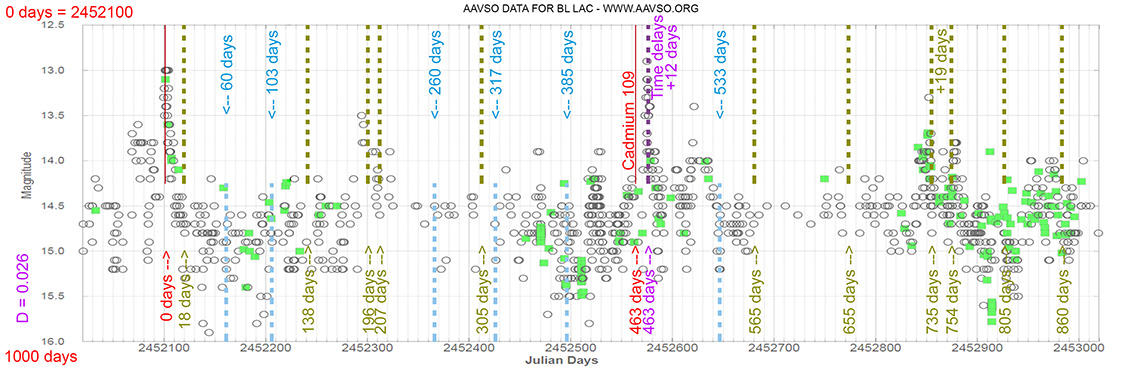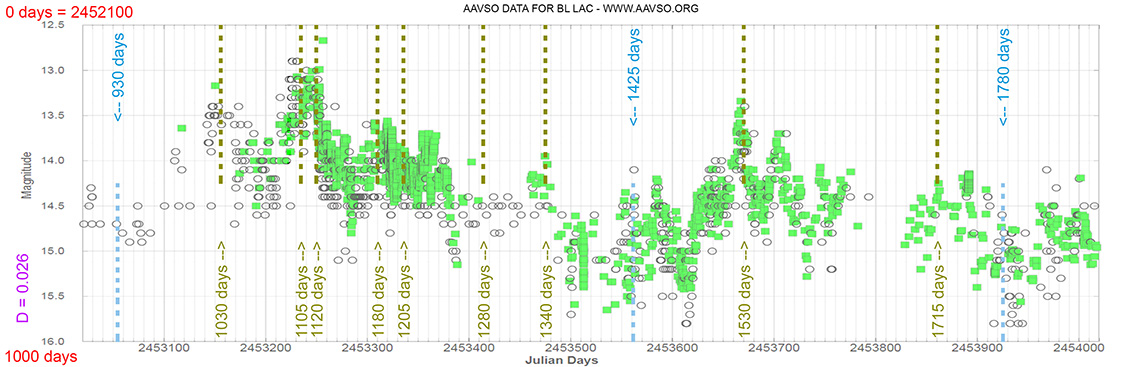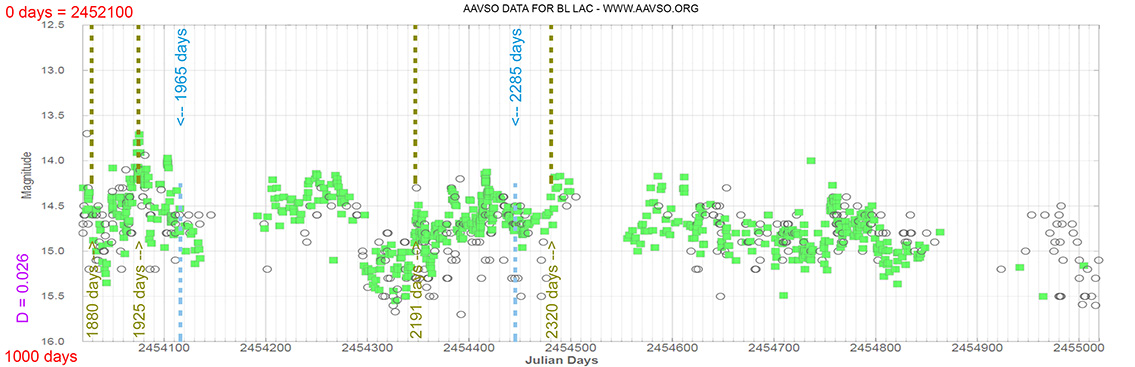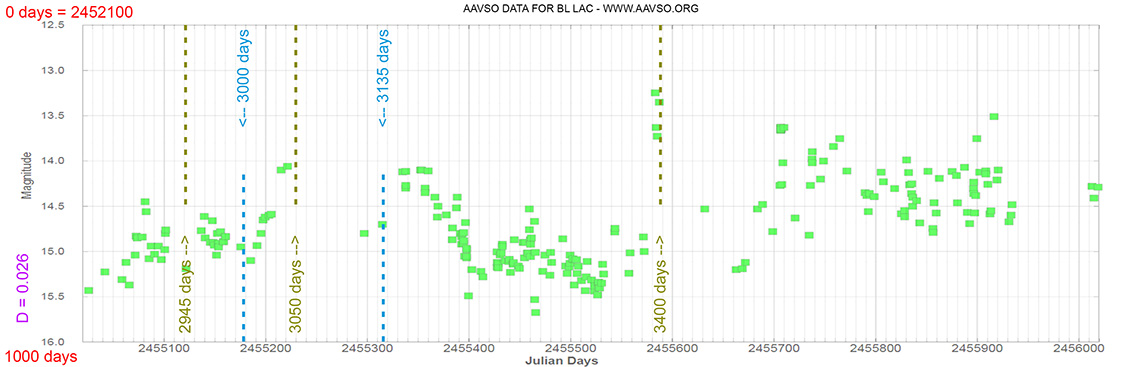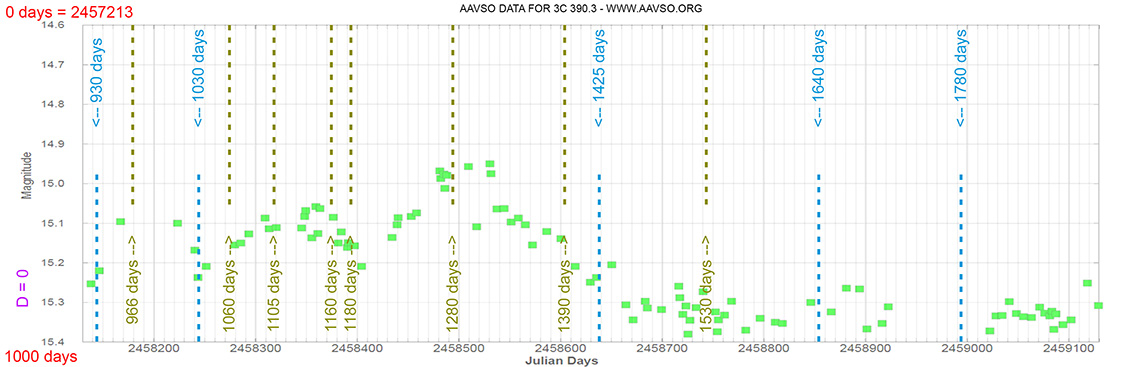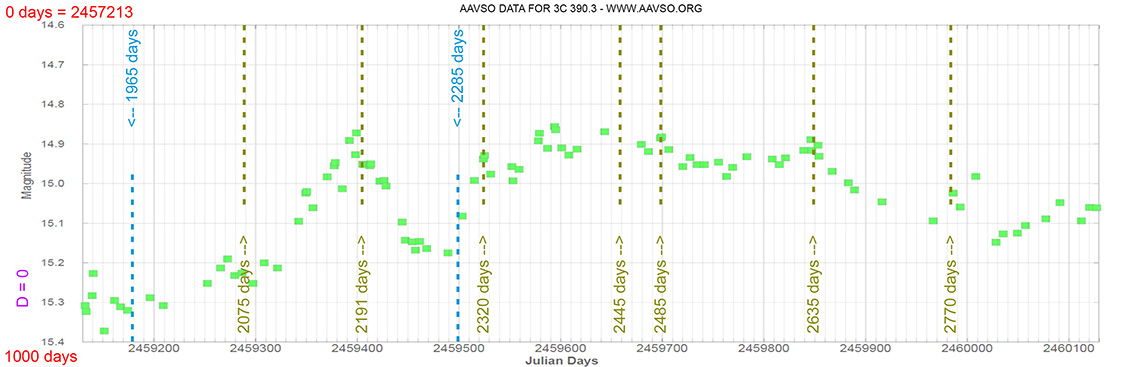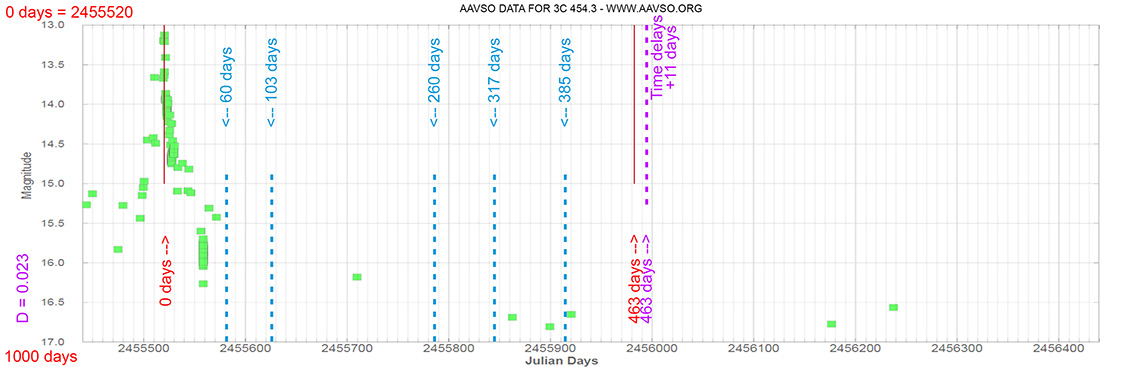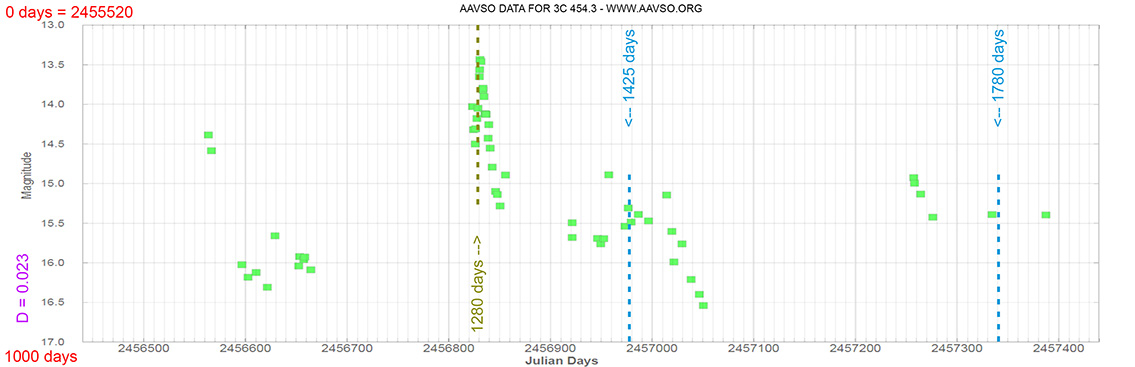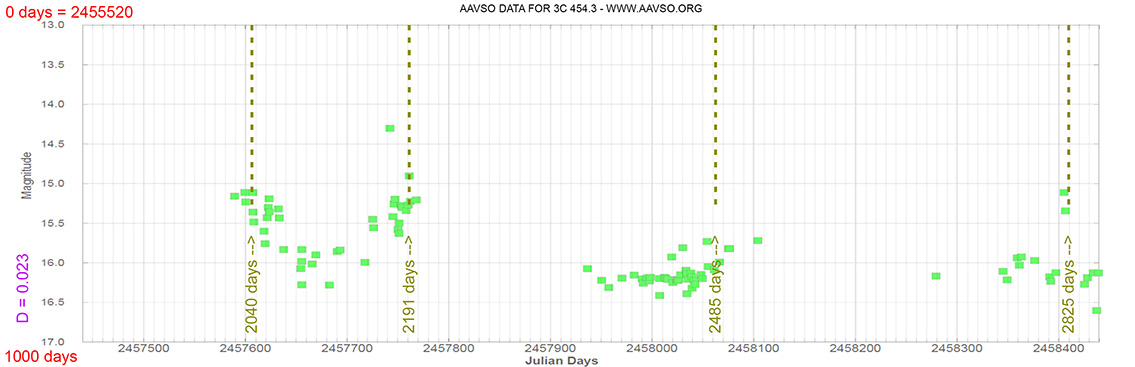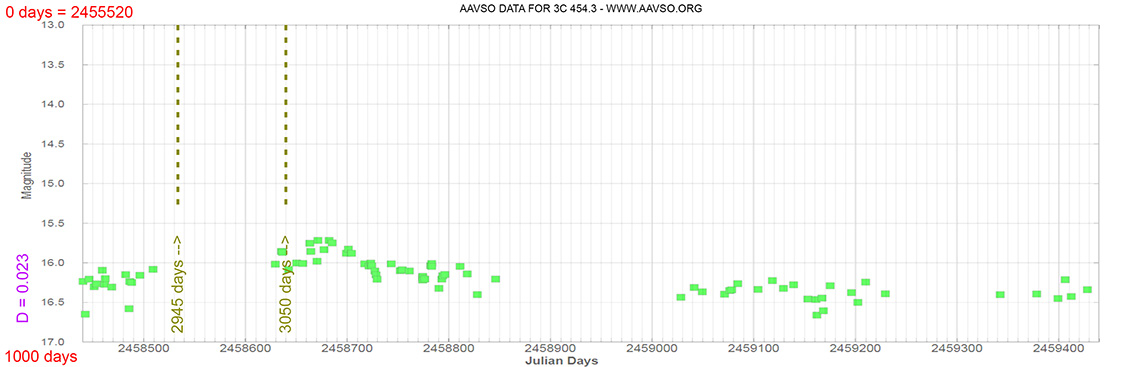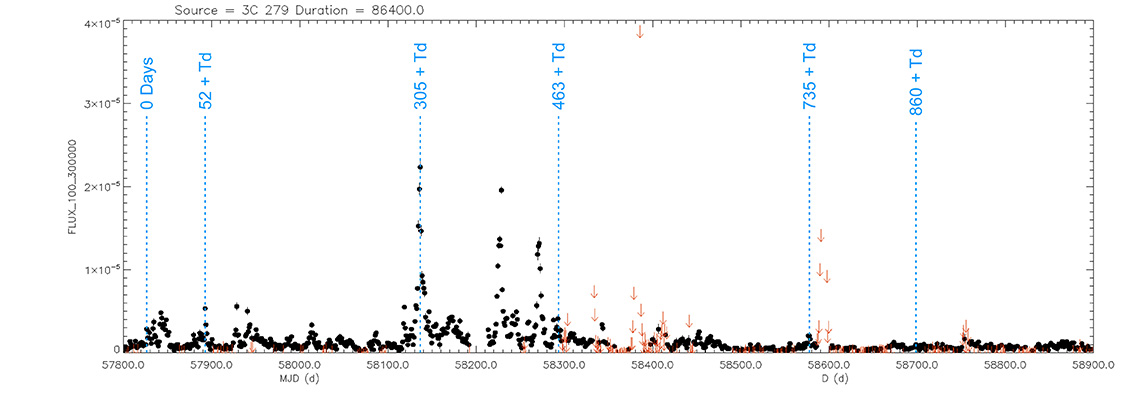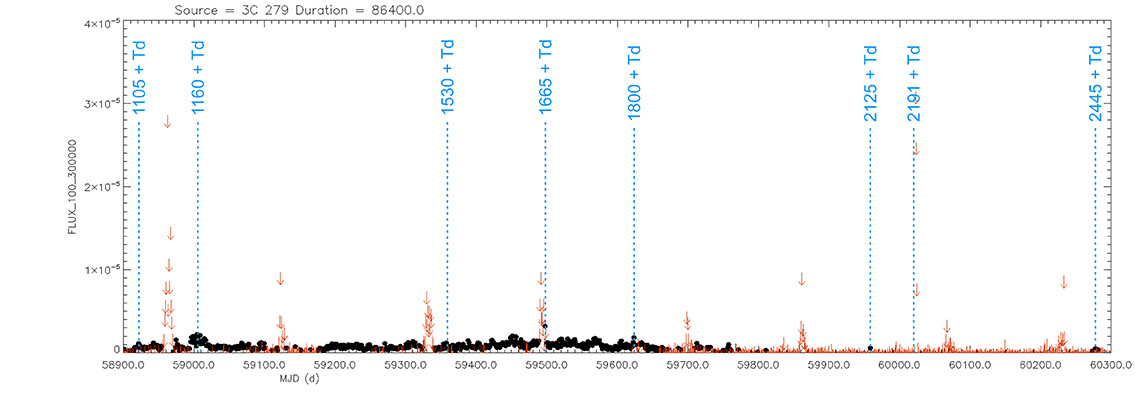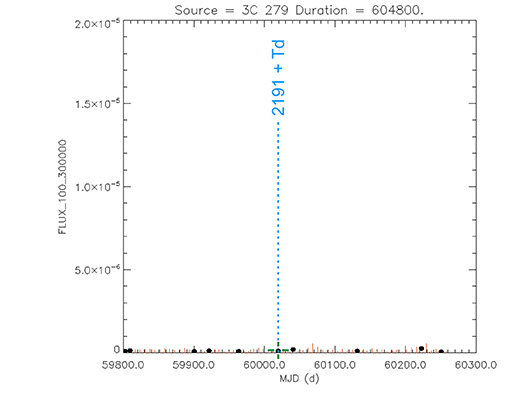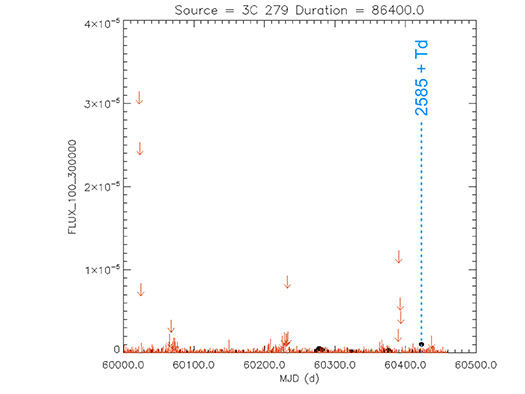Time Delay Outburst Type I Blazar BL LAC (22 02 43.29139 +42 16 39.9803) z=0.069 Outburst Type I Seyfert 1 Galaxy 3C 390.3 (18 42 08.9899 +79 46 17.128) z=0.056159 Outburst Type I Quasar 3C 454.3 (22 53 57.74798 +16 08 53.5611) z=0.859001 Outburst Type I Quasar 3C 279 (12 56 11.16657 -05 47 21.5247) z=0.53620 Light curve. NASA's Fermi Gamma-ray Space Telescope Outburst Type II Blazar S5 2007+77 (20 05 31.004 +77 52 43.27) z=0.342 The Astronomer’s Telegram. Nº 8635 Burst Gamma ray. 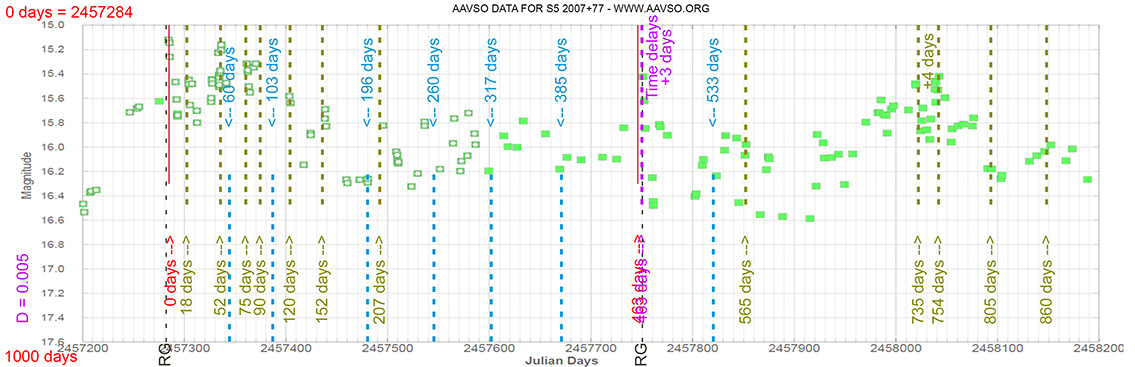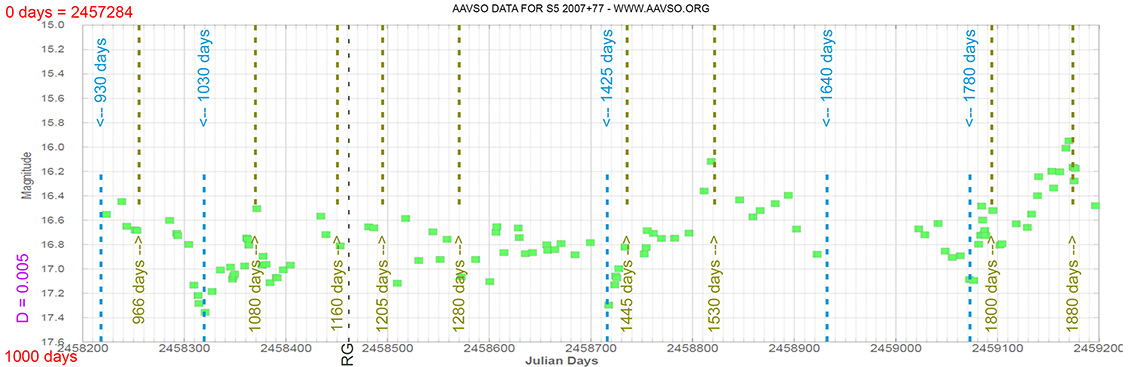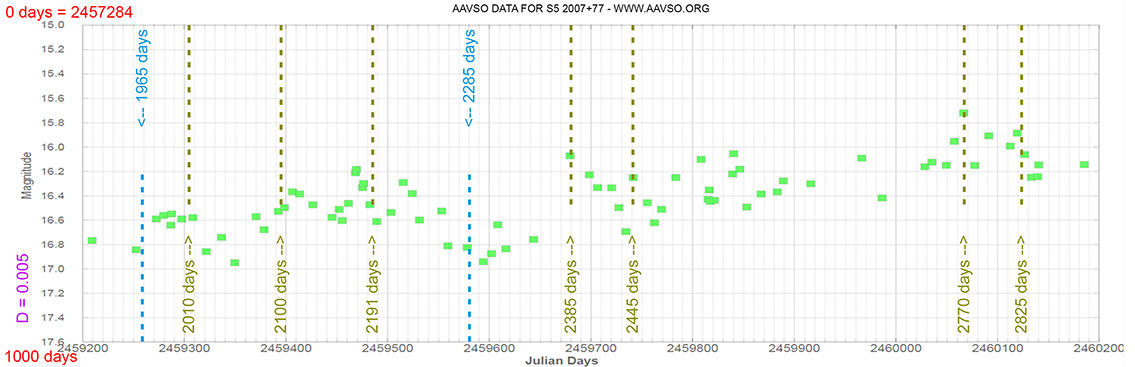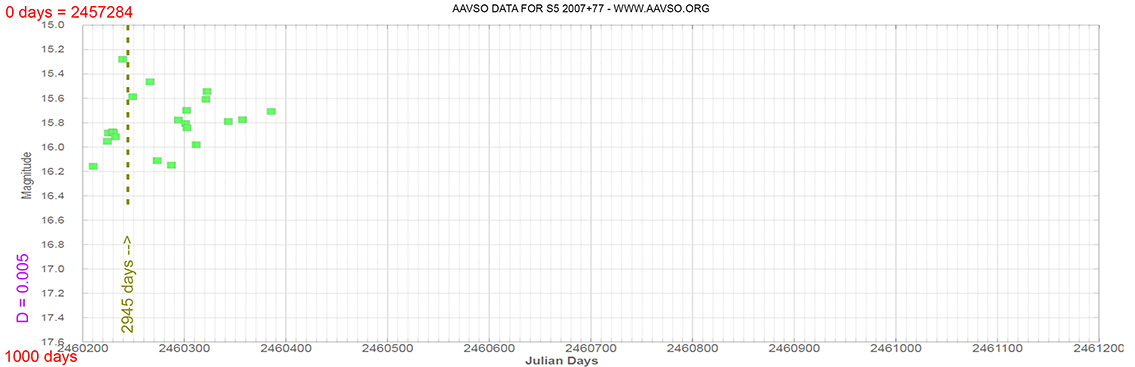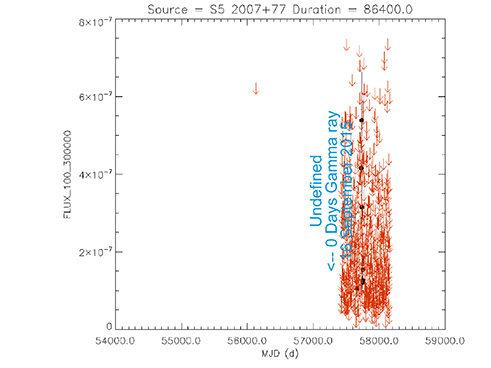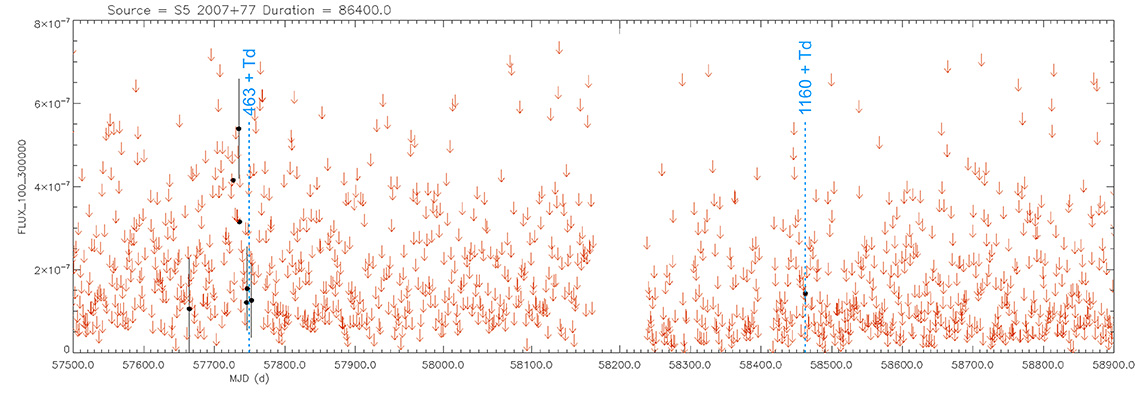4 Feb 2016 Light curve. 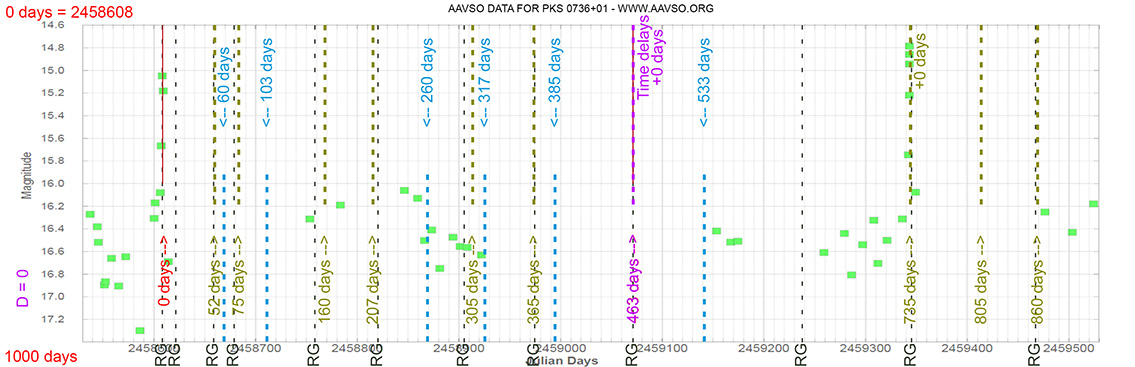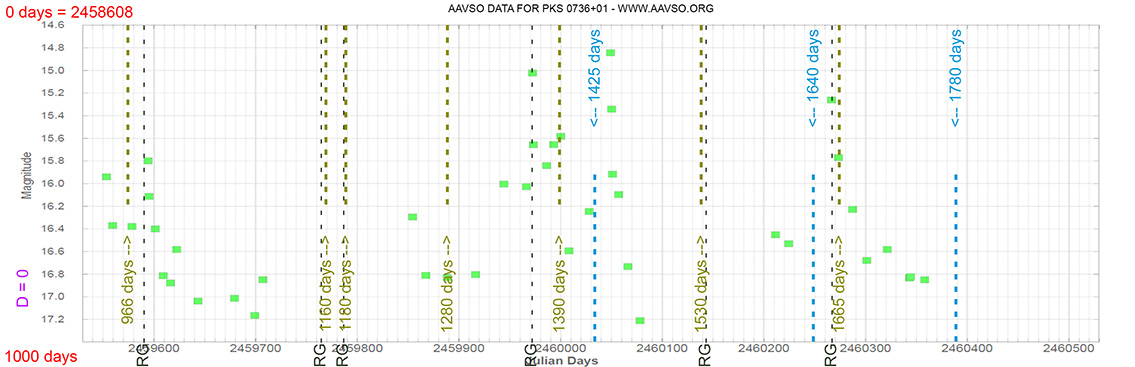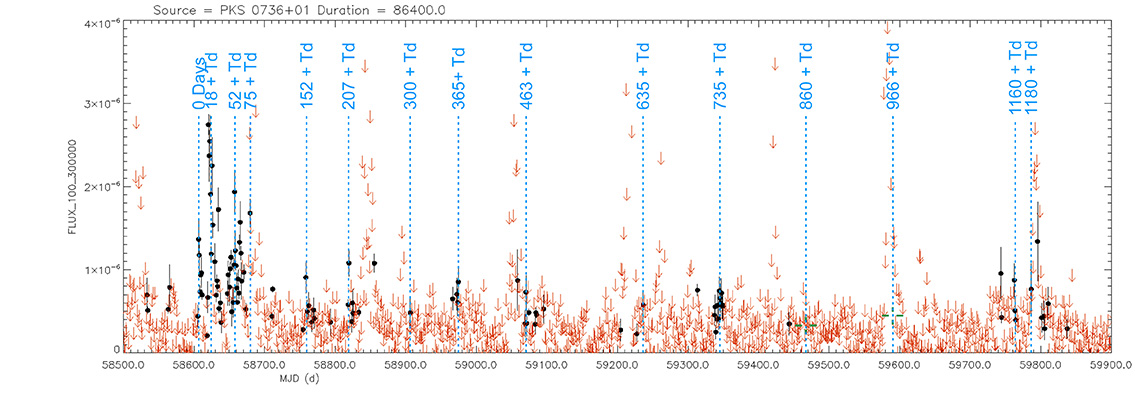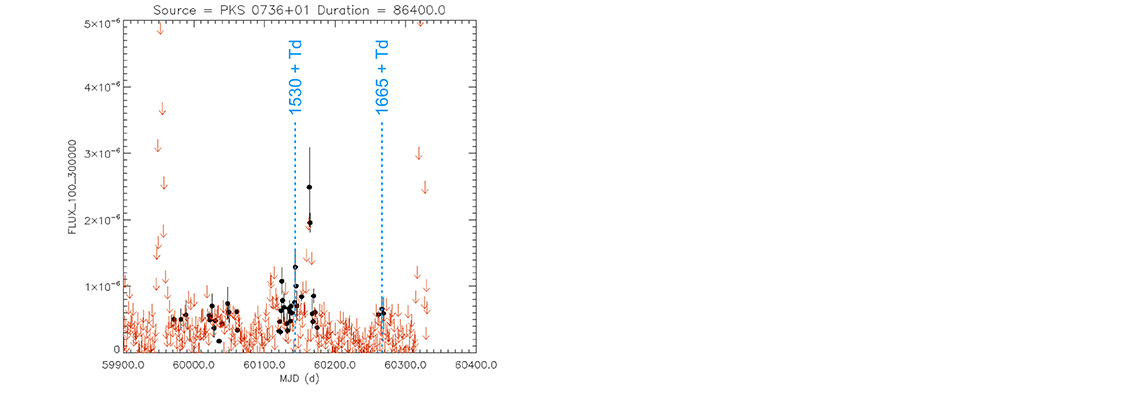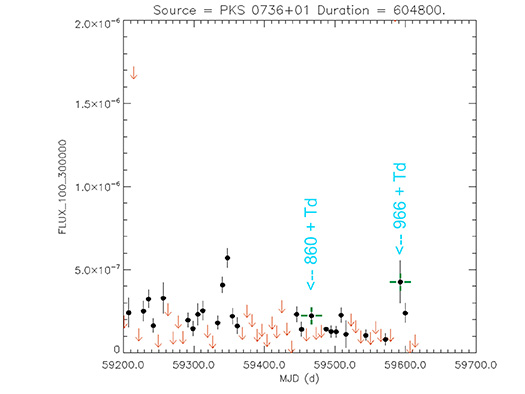NASA's Fermi Gamma-ray Space Telescope Outburst Type II Quasar PKS 0736+01 (07 39 18.03390 +01 37 04.6179) z=0.191 Light curve. 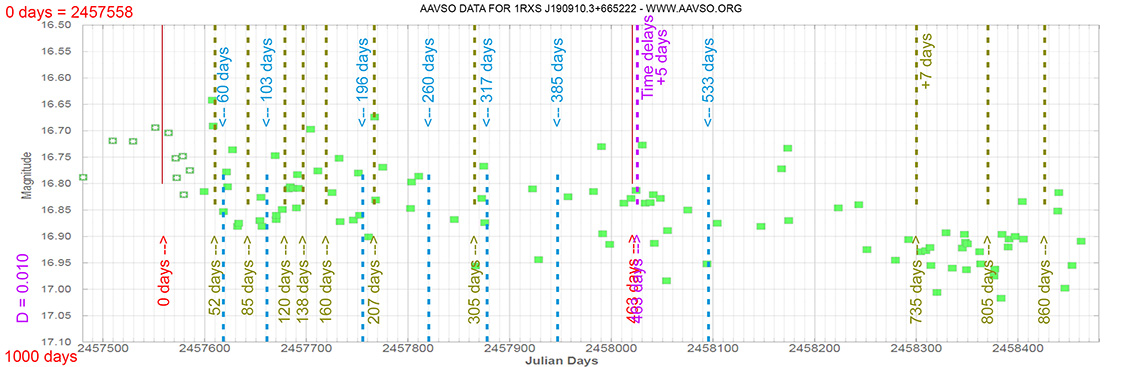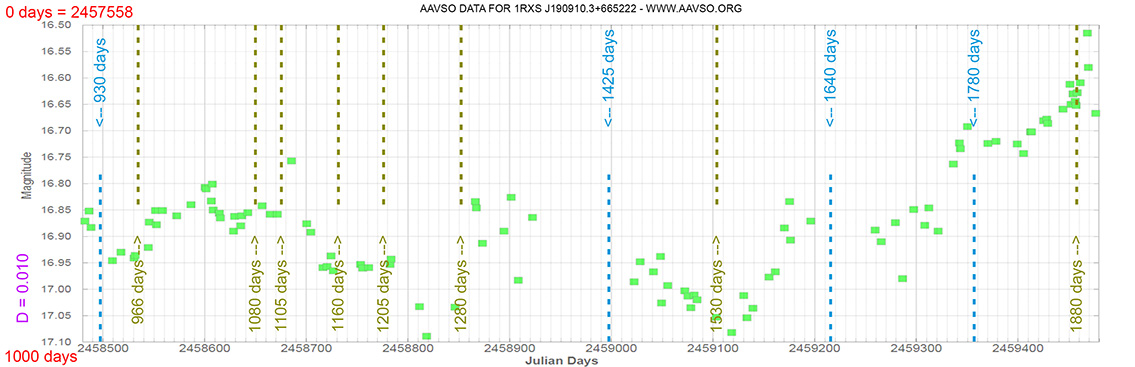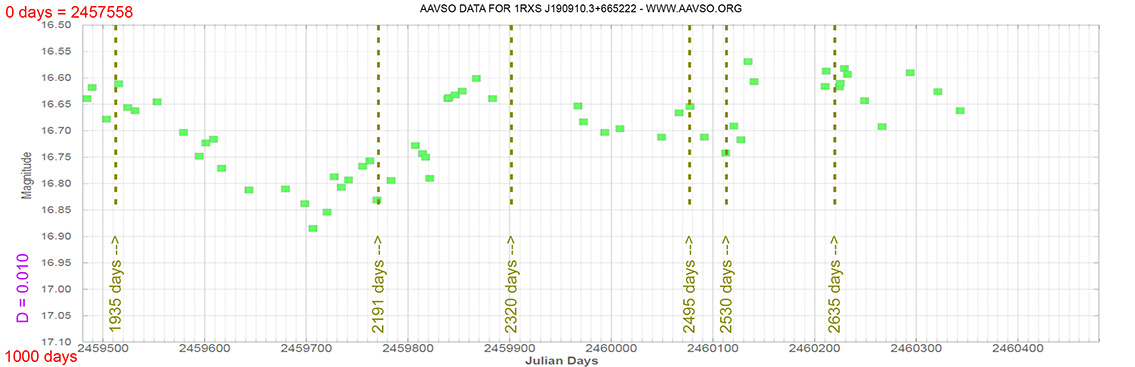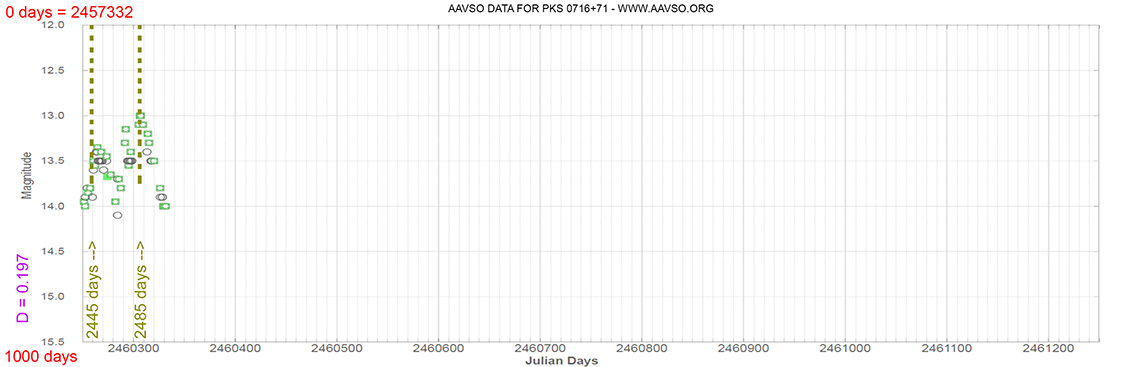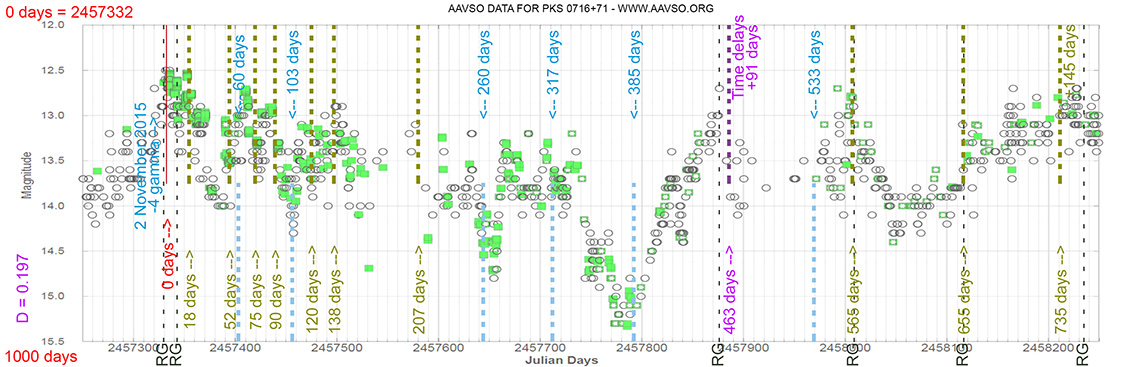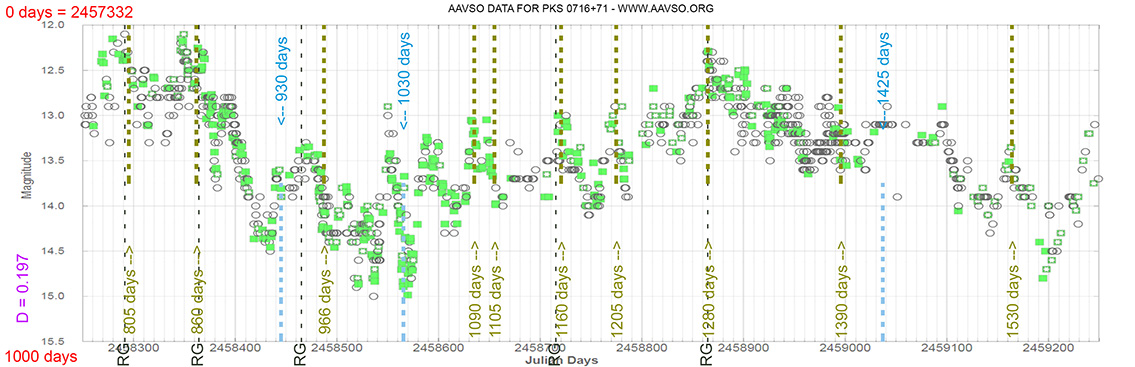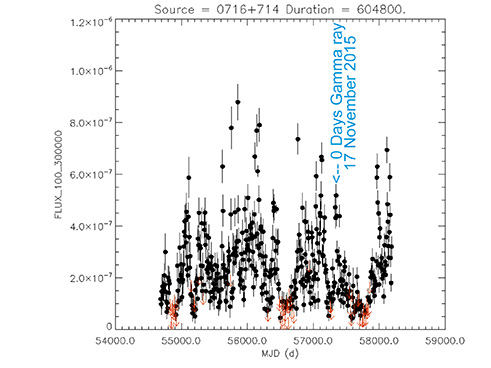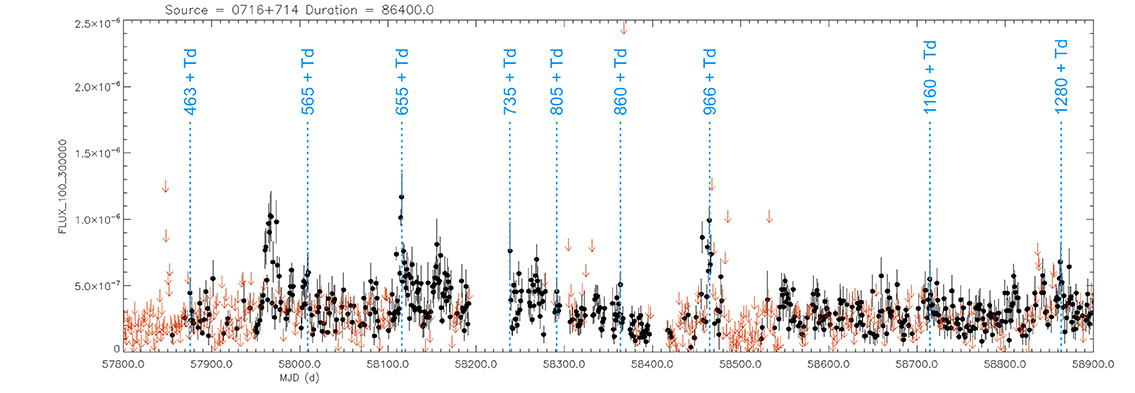NASA's Fermi Gamma-ray Space Telescope Outburst Type III Seyfert 1 Galaxy 1RXS J190910.3+665222 (19 09 10.8964 +66 52 21.373) z=0.191 Outburst Type II Blazar PKS 0716+71 (07 21 53.44846 +71 20 36.3634) z=0.300 Light curve. 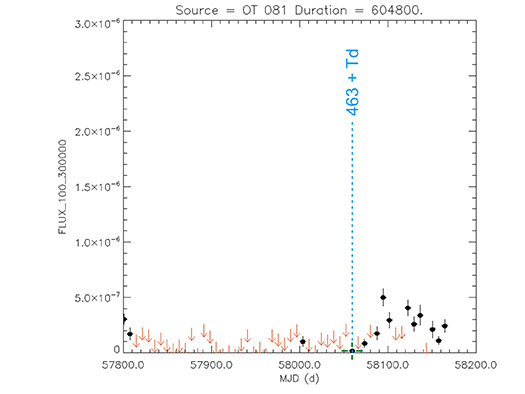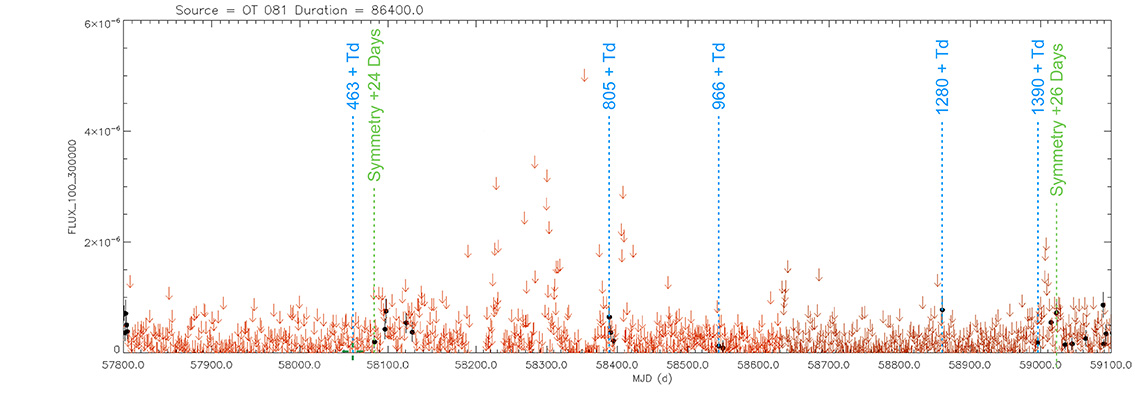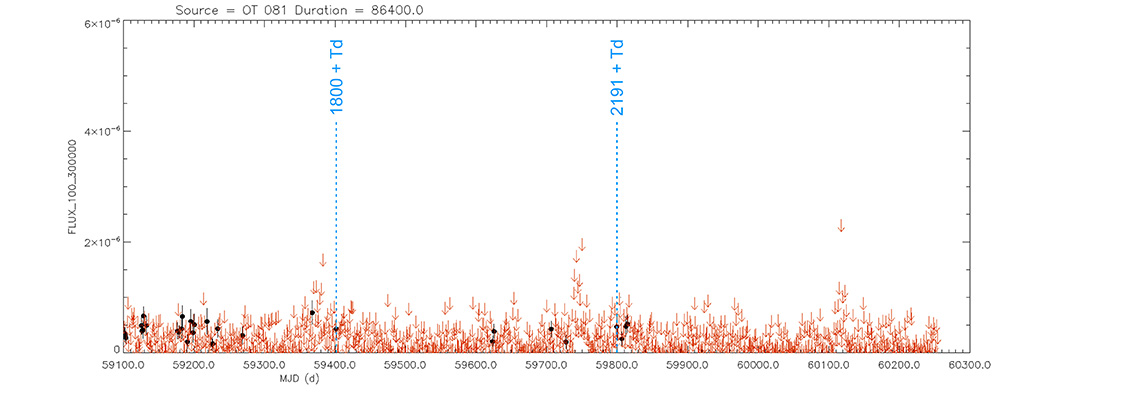NASA's Fermi Gamma-ray Space Telescope Outburst Type III Blazar OT 081 (17 51 32.81855 +09 39 00.7288) z=0.322 Light curve. 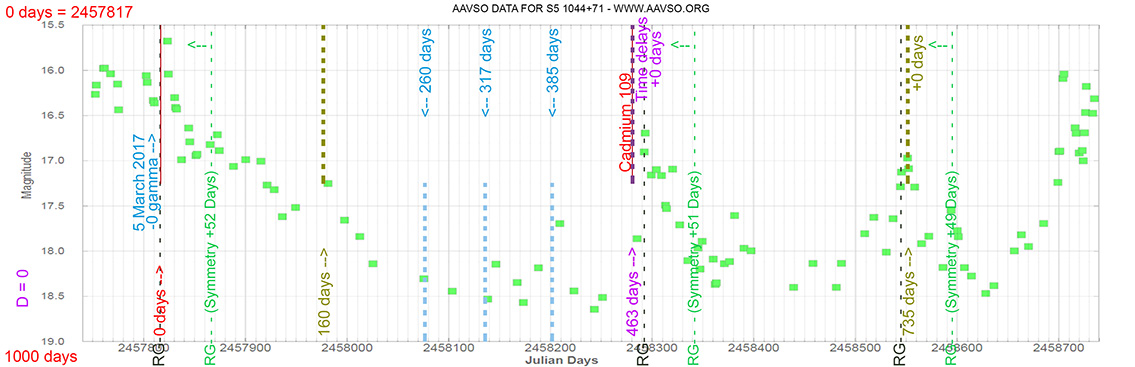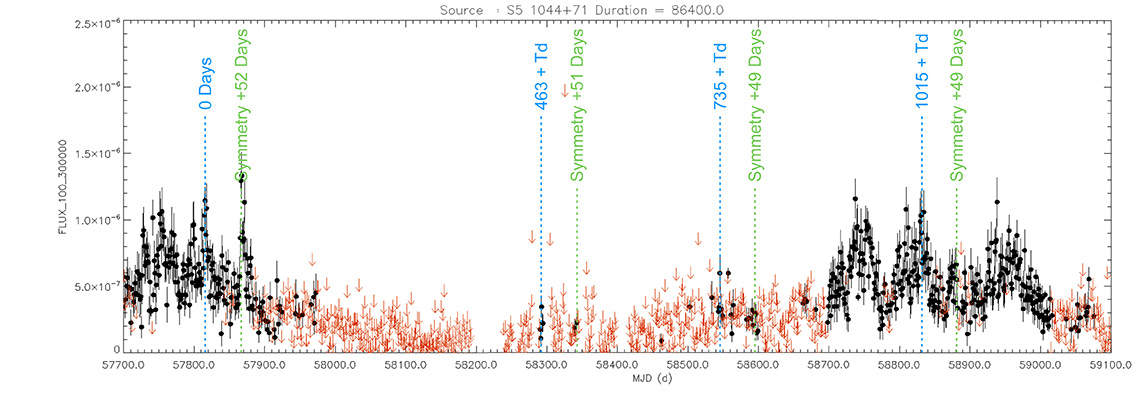NASA's Fermi Gamma-ray Space Telescope Outburst Type II Quasar S5 1044+71 (10 48 27.6 +71 43 36) z=1.1500 Light curve. NASA's Fermi Gamma-ray Space Telescope Outburst Type III Blazar S5 1803+78 (18 00 45.684 +78 28 04.02) z=0.680 The Astronomer’s Telegram. Nº 7933 Burst Gamma ray. 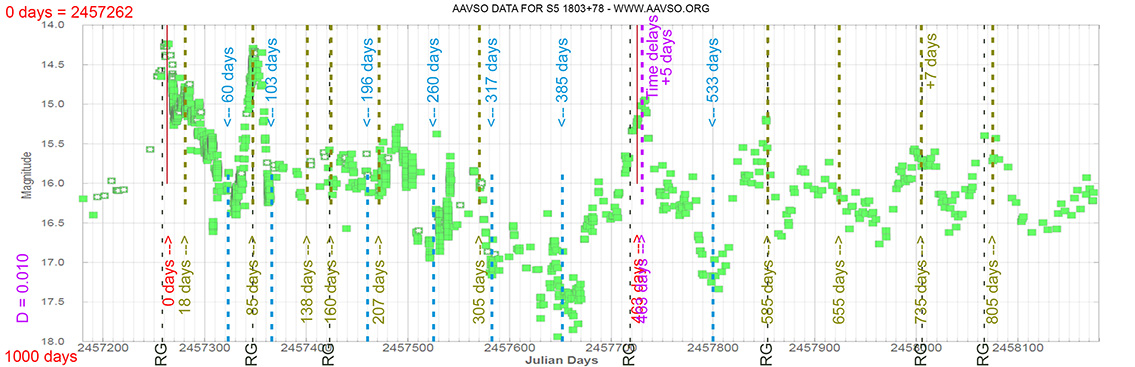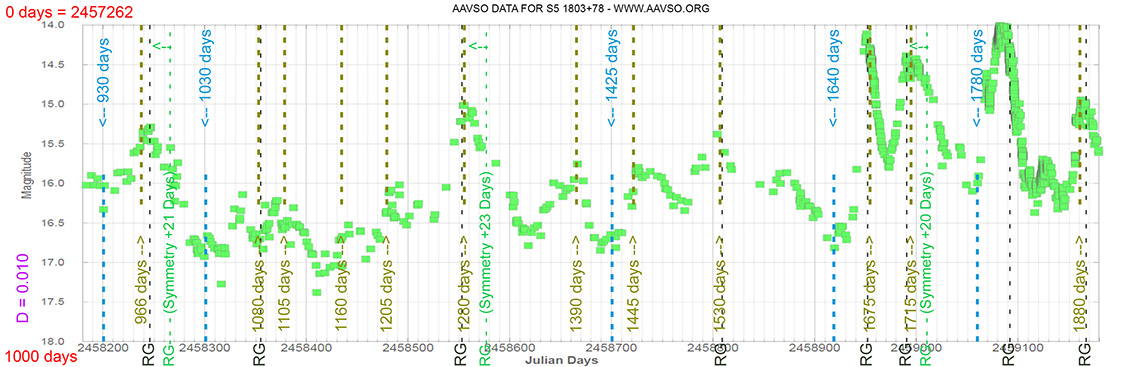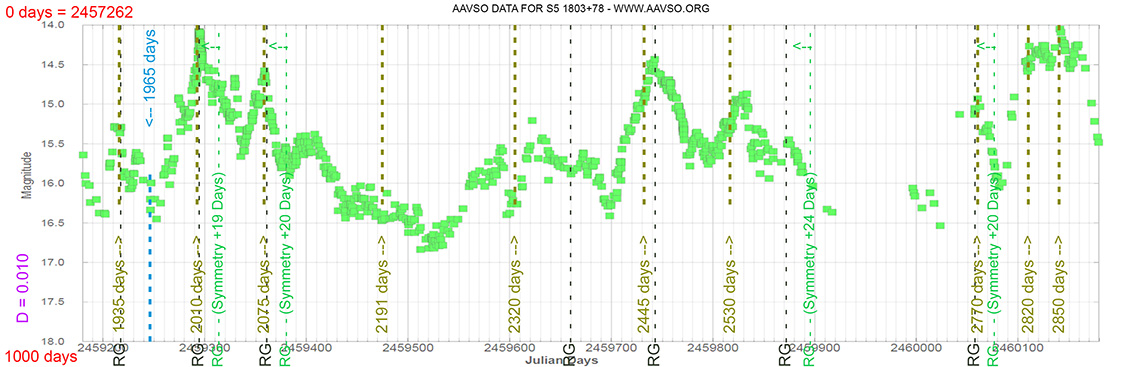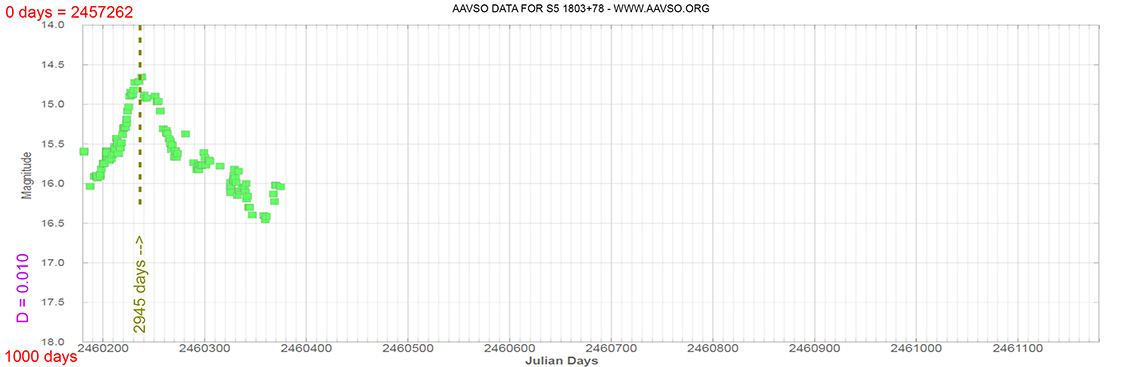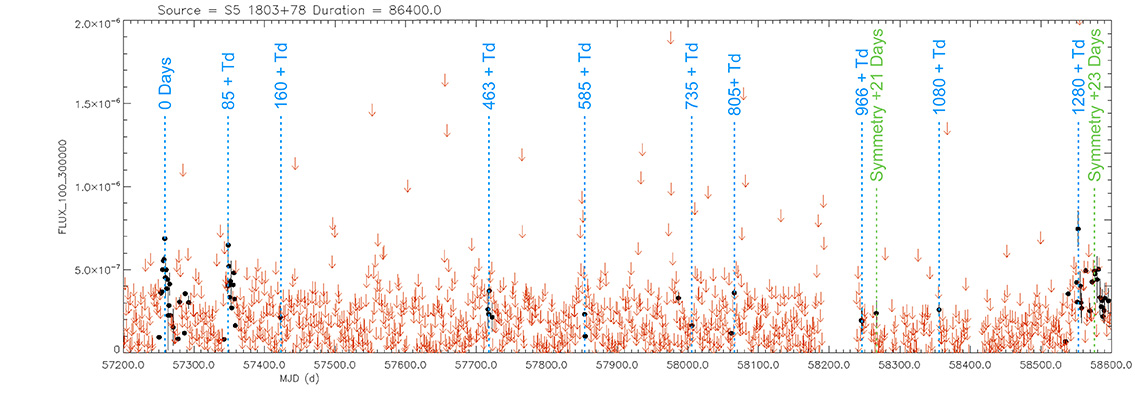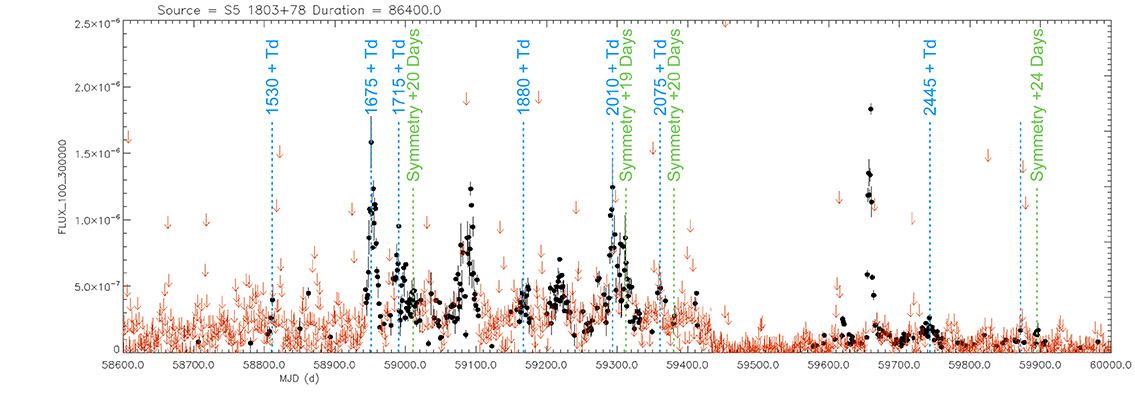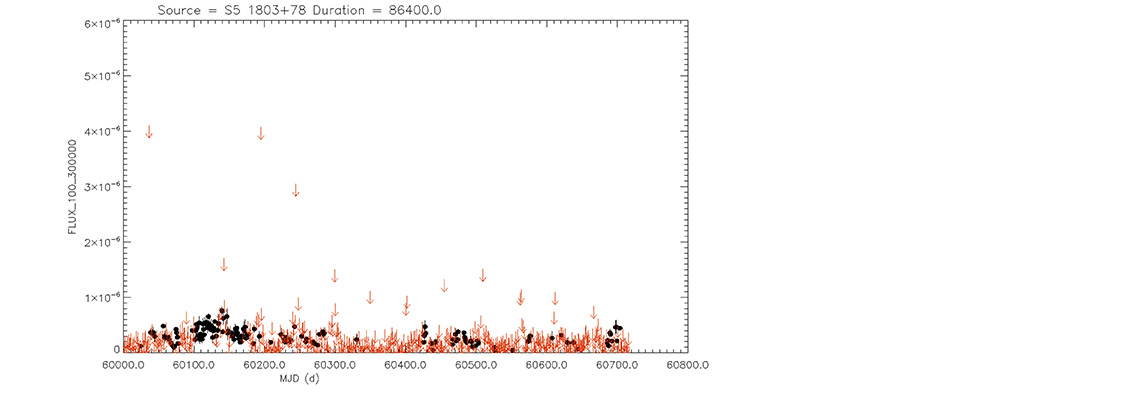20 Aug 2015 Light curve. 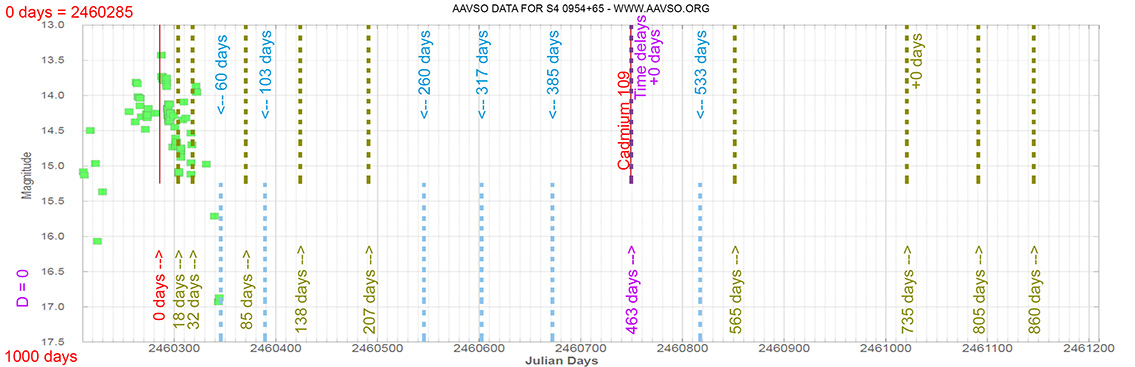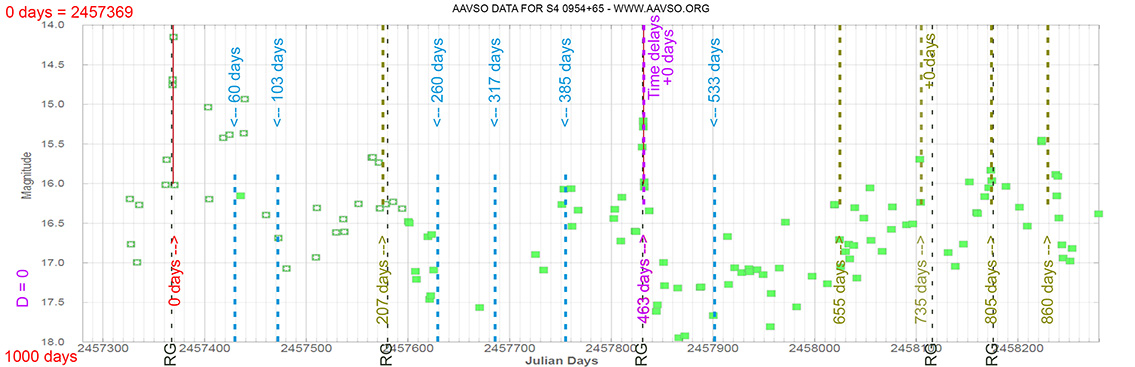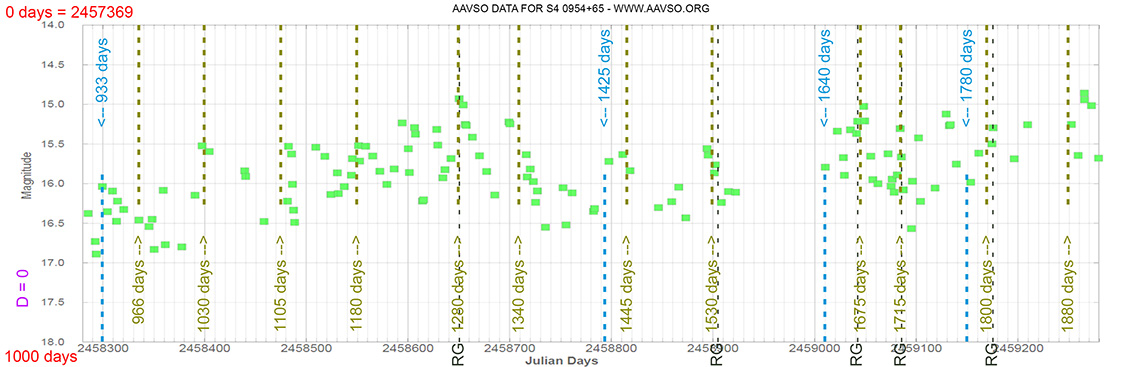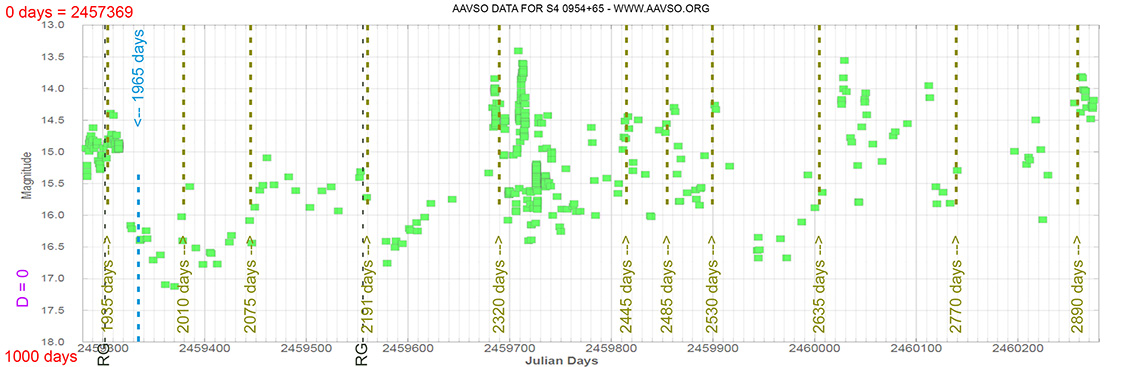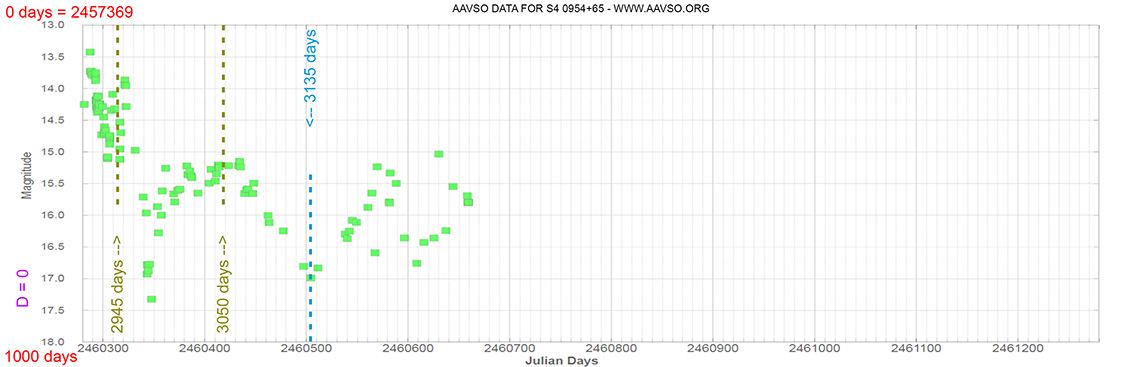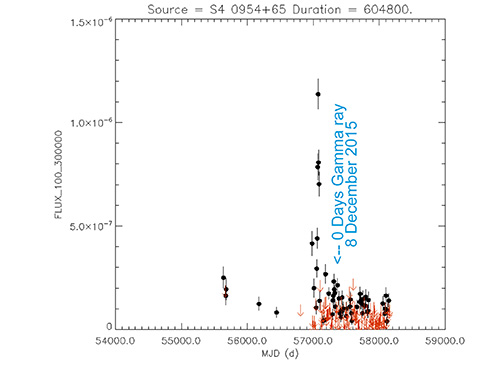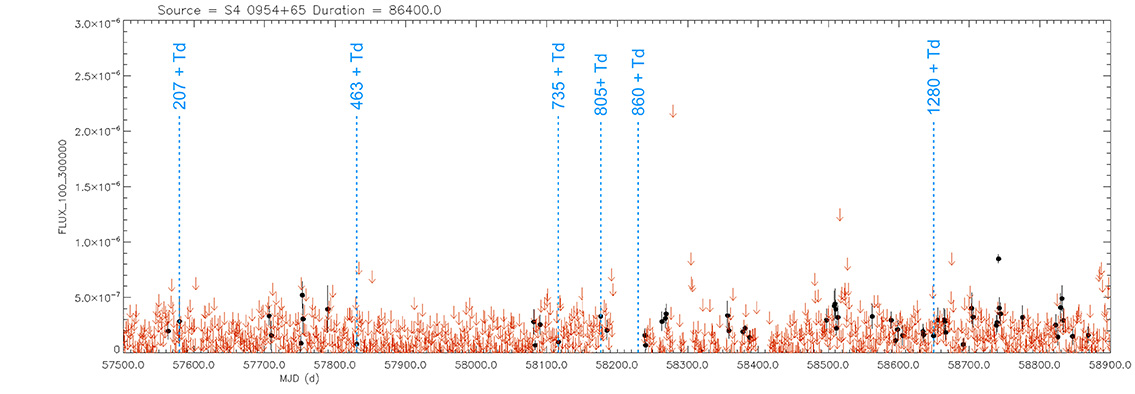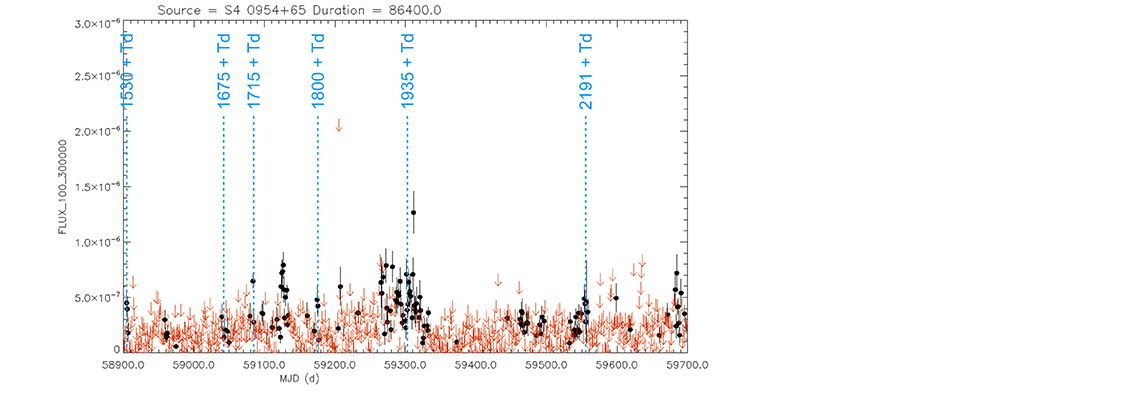NASA's Fermi Gamma-ray Space Telescope Outburst Type III Blazar S4 0954+65 (09 58 47.24510 +65 33 54.8181) z=0.367 Light curve. 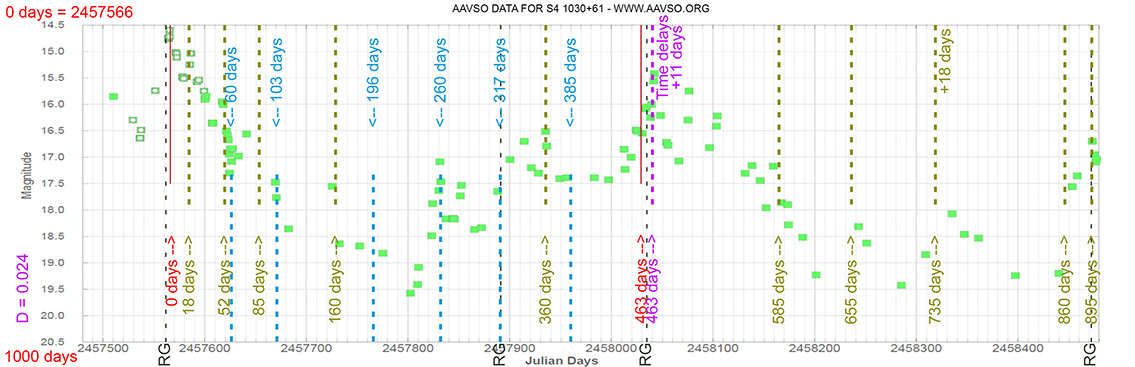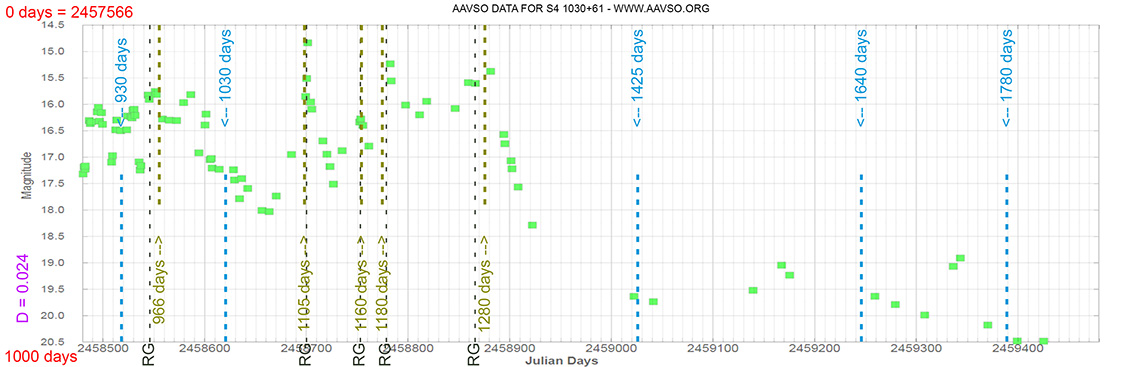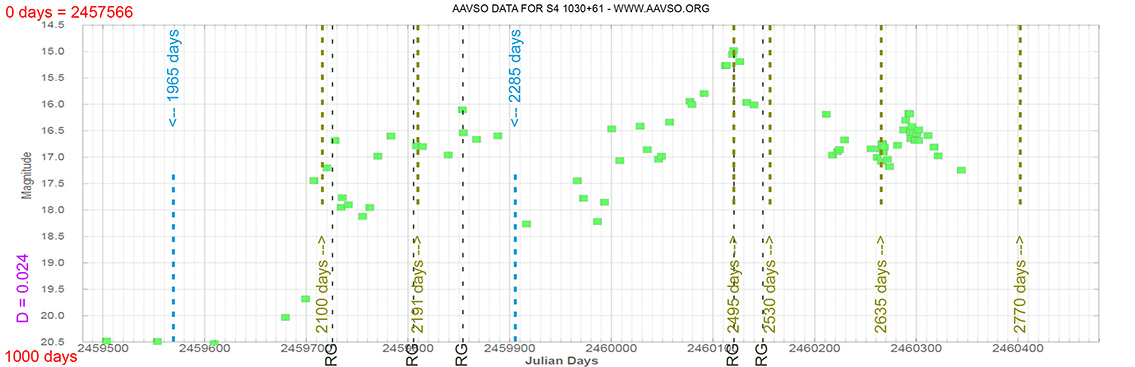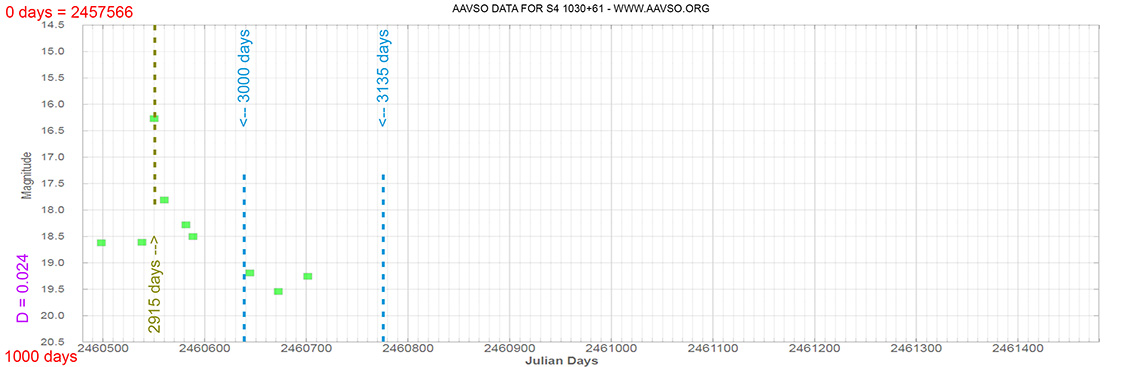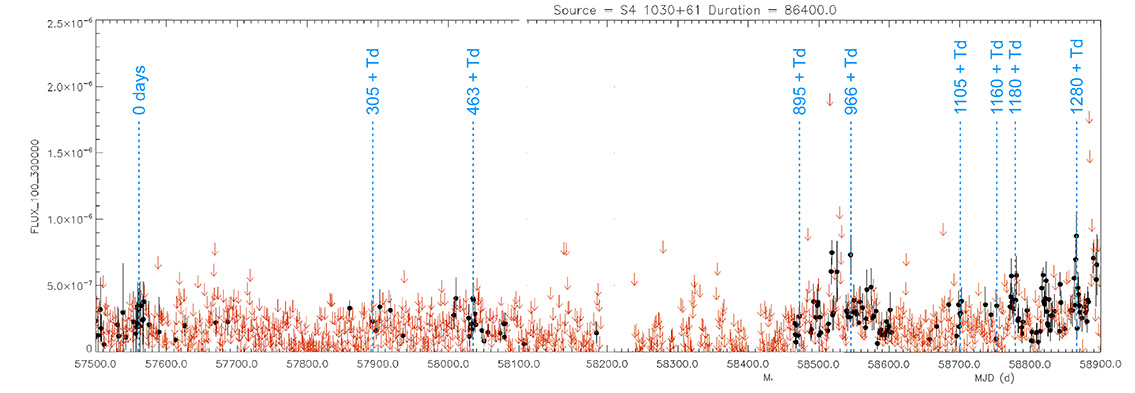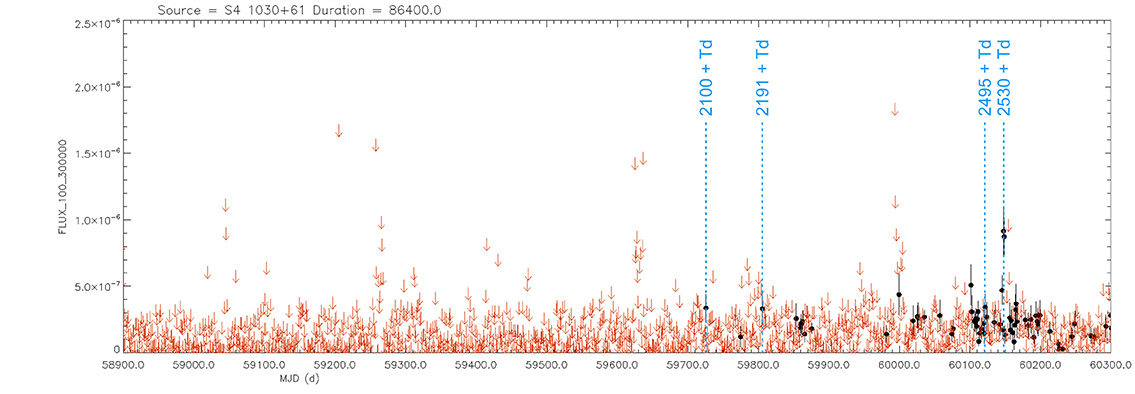NASA's Fermi Gamma-ray Space Telescope Outburst Type III Seyfert 1 Galaxy S4 1030+61 (10 33 51.42726 +60 51 07.3301) z=1.40095 Light curve. NASA's Fermi Gamma-ray Space Telescope Outburst Type III Blazar OJ 287 (08 54 48.87493 +20 06 30.6410) z=0.306 The Astronomer’s Telegram. Nº 9489 Burst Gamma ray. 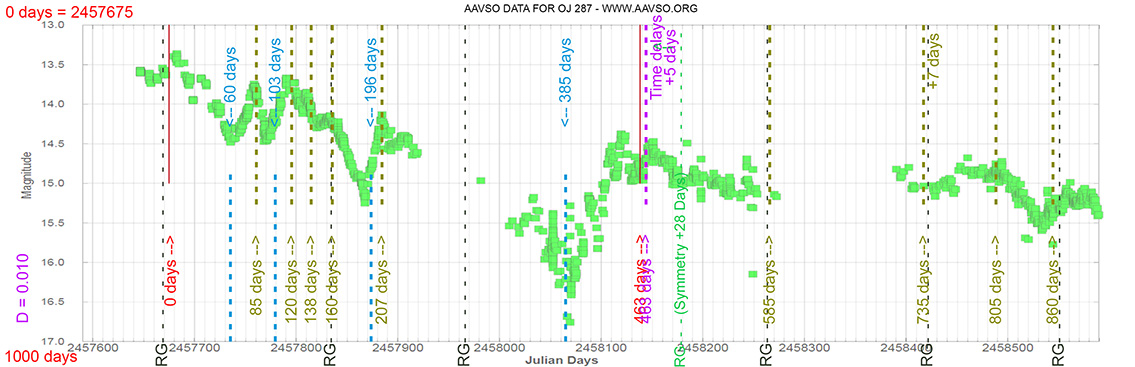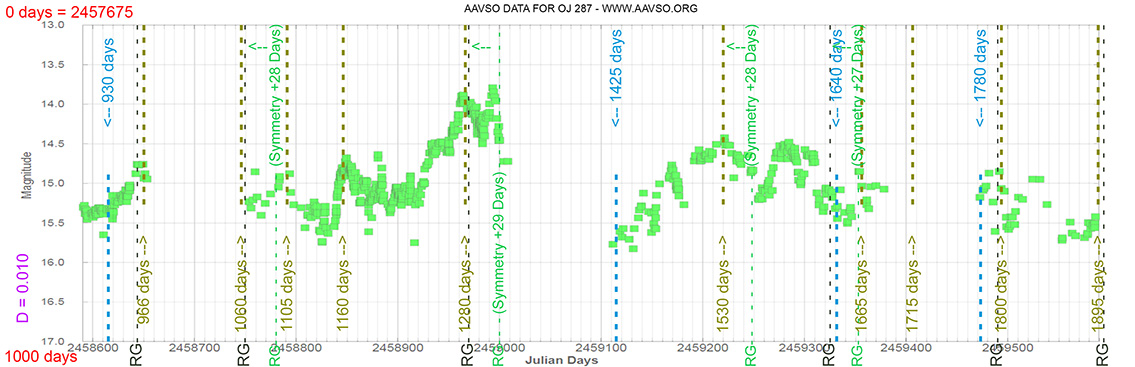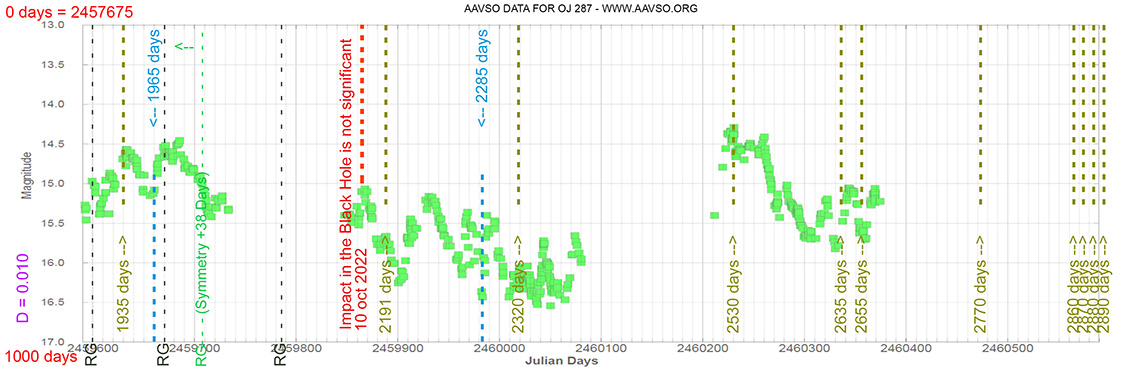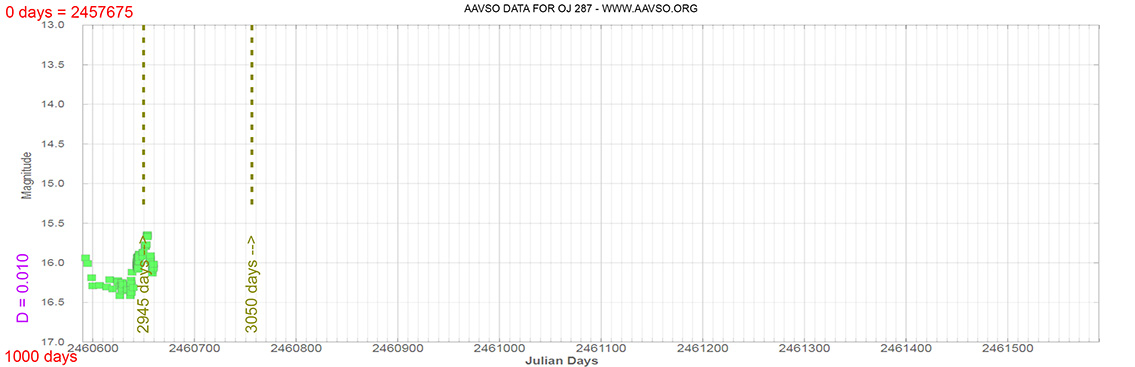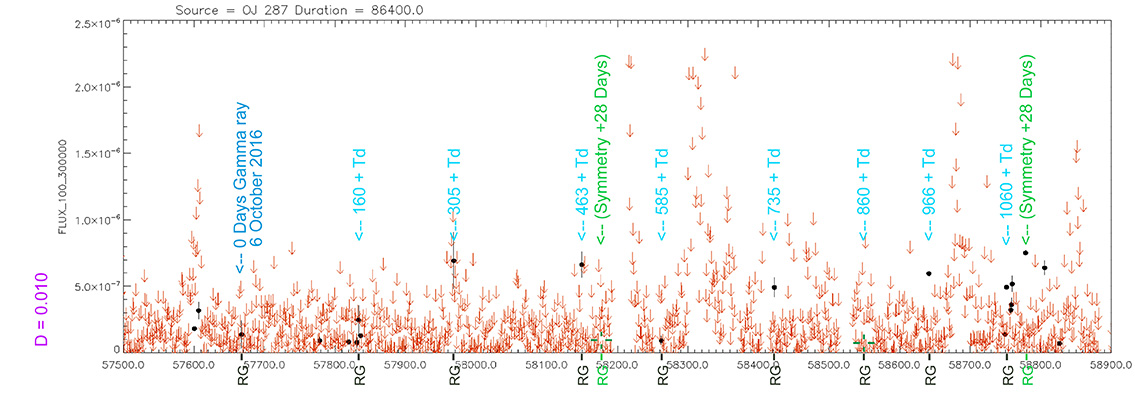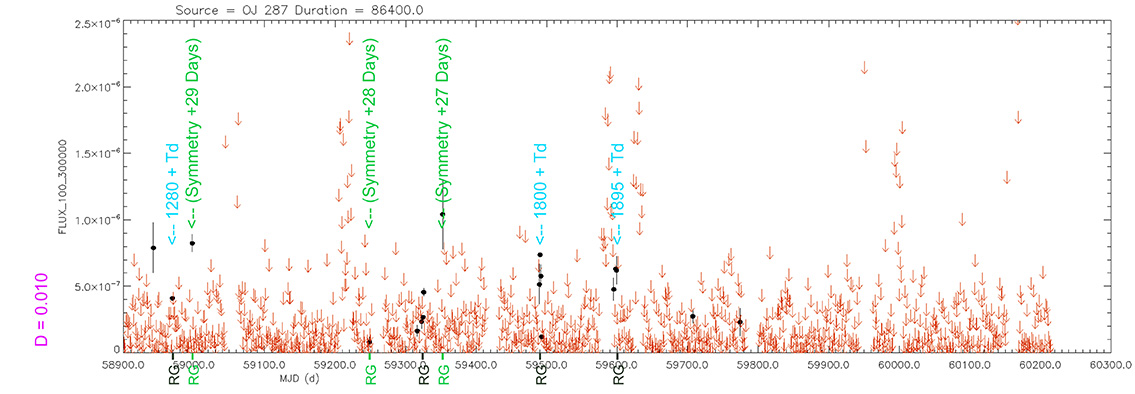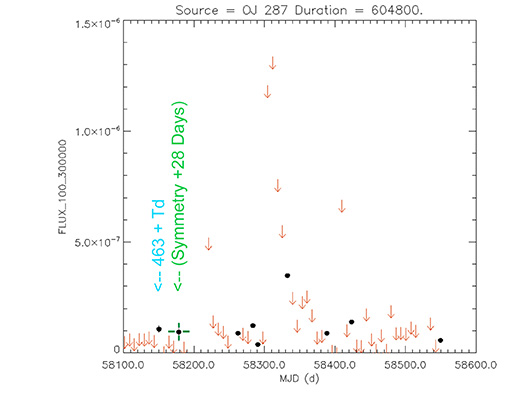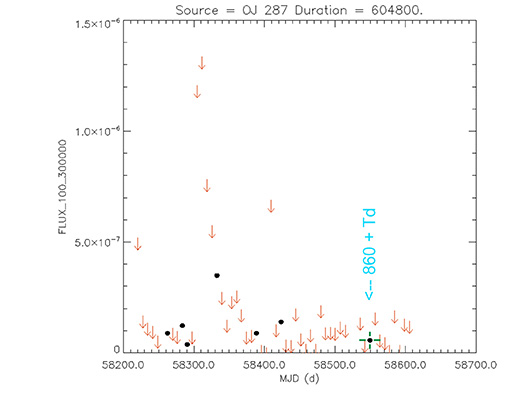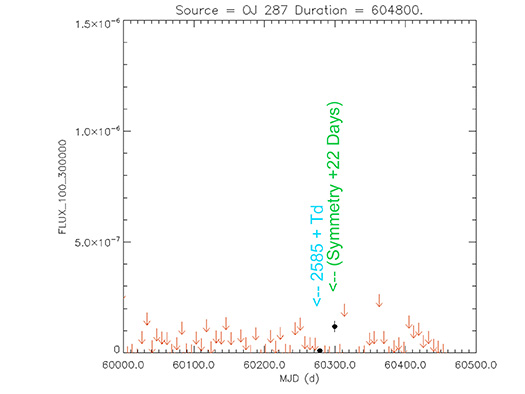13 Sep 2016 Light curve. 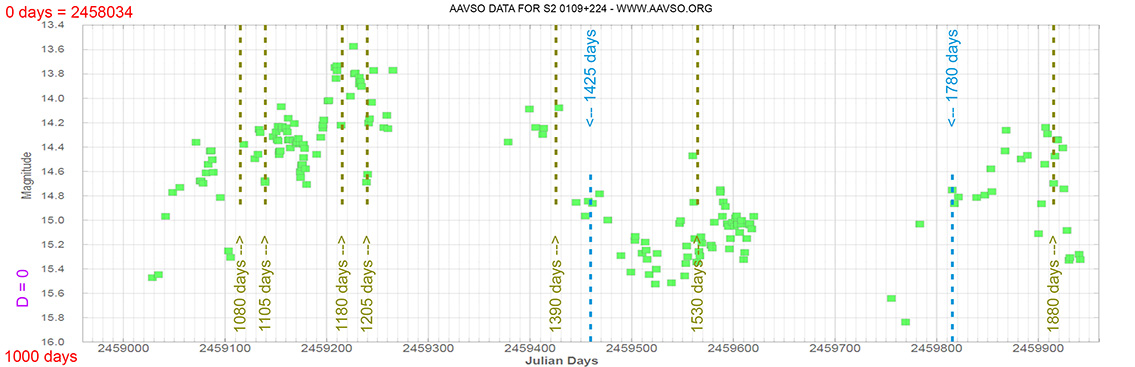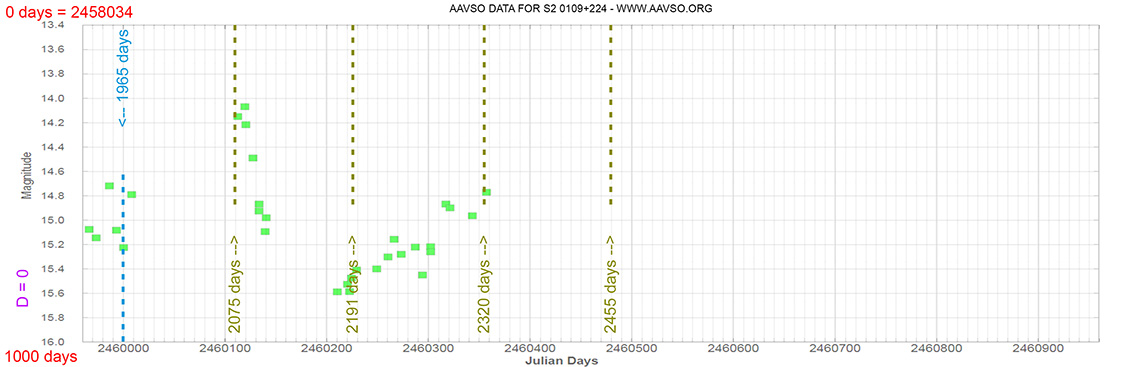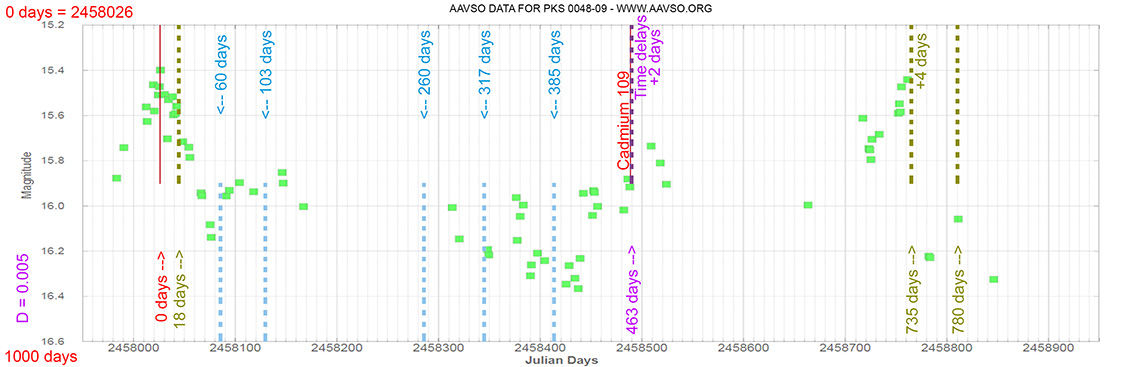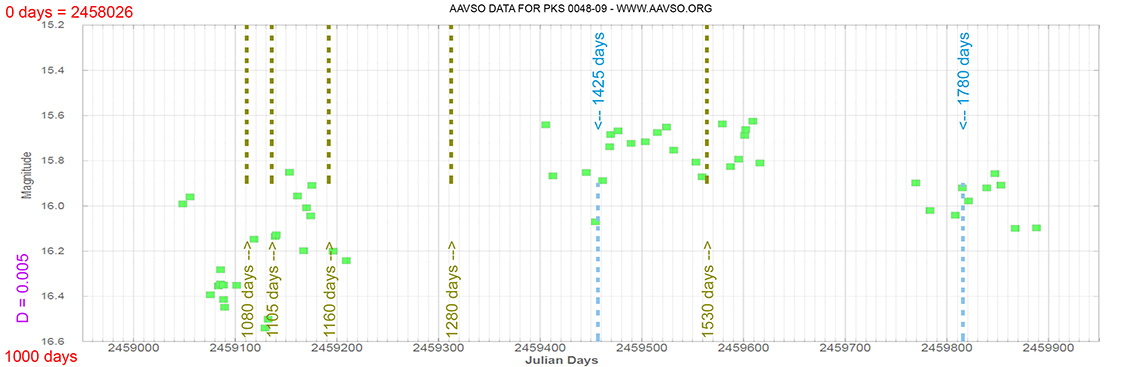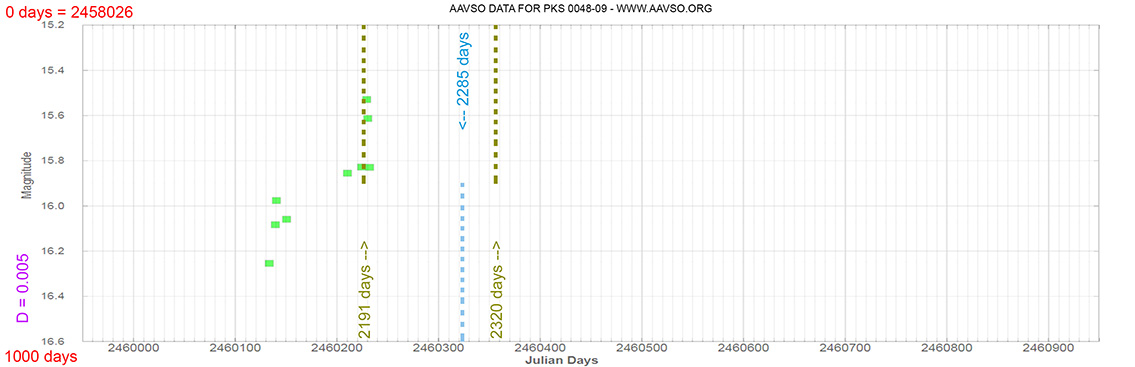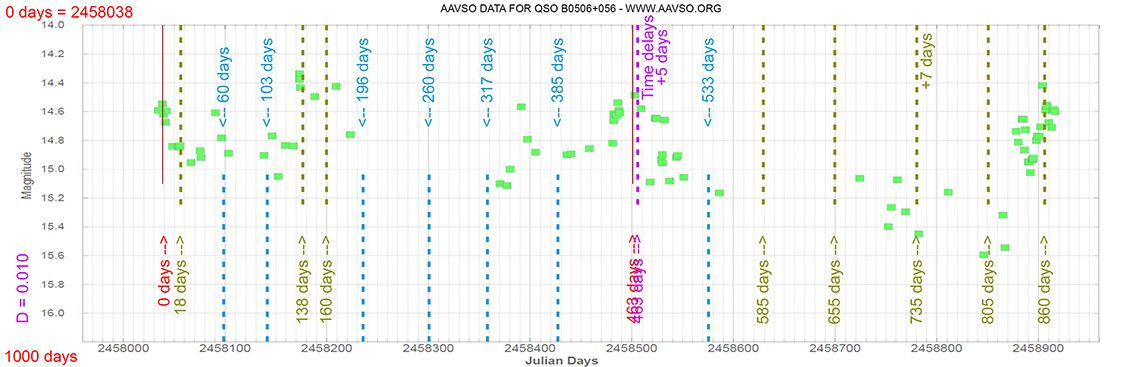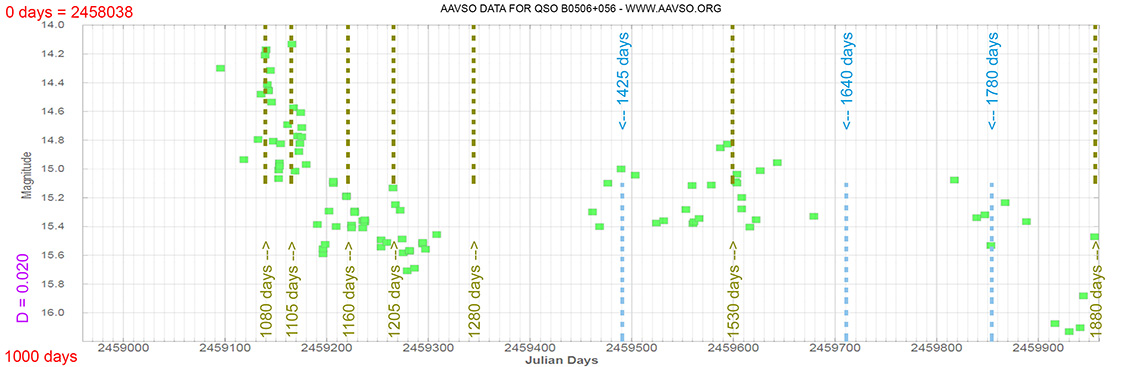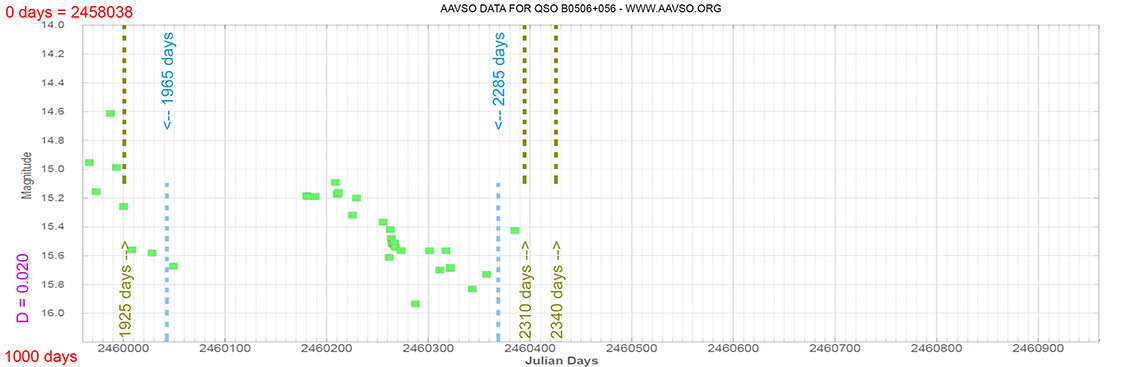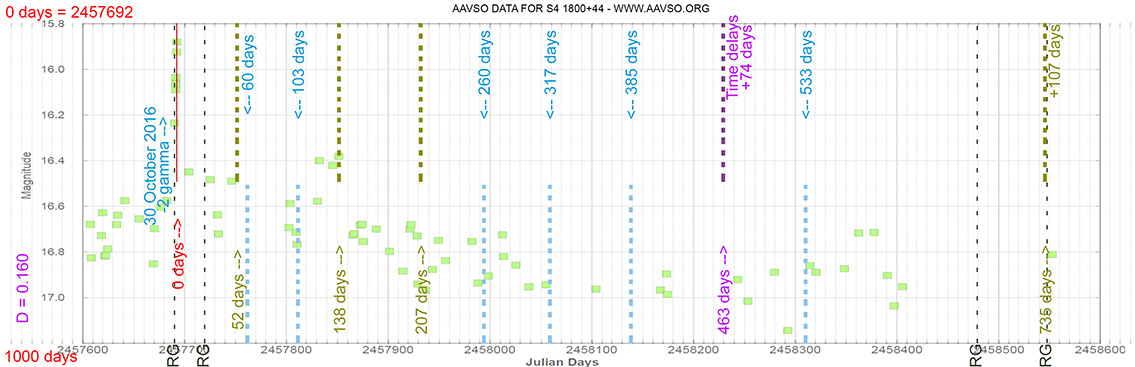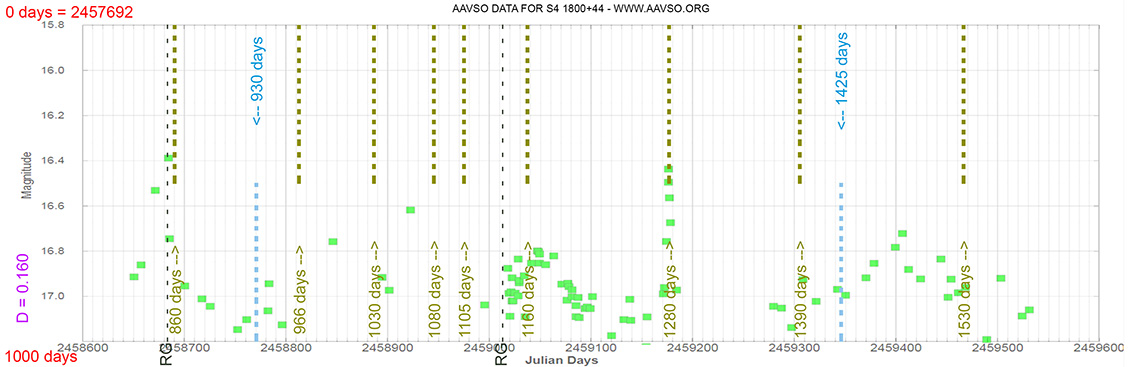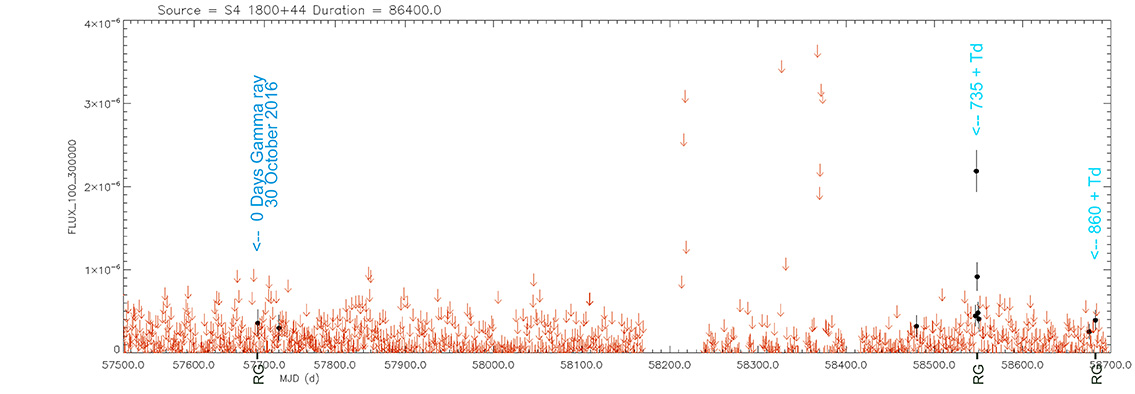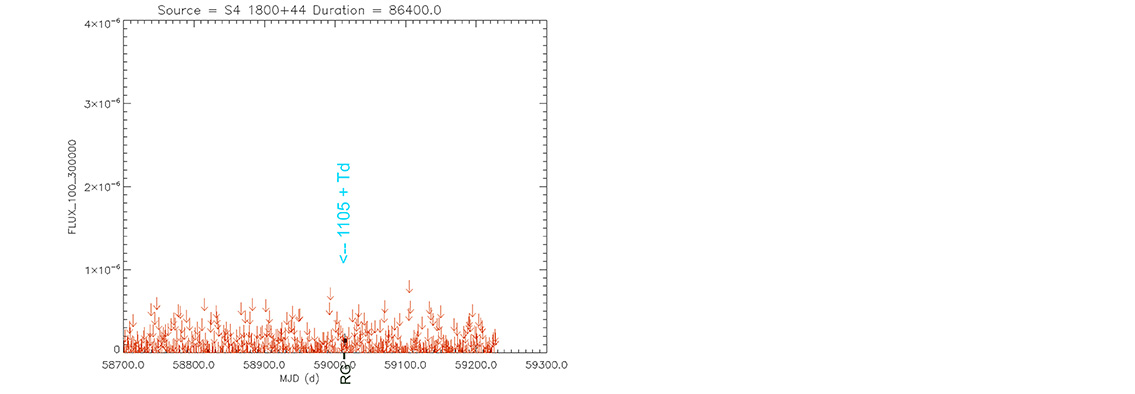NASA's Fermi Gamma-ray Space Telescope Outburst Type III Blazar S2 0109+224 (01 12 05.82470 +22 44 38.7868) z=0.265 Outburst Type I Blazar PKS 0048-09 (00 50 41.31738756 -09 29 05.2102688) z=0.635 Outburst Type II Blazar QSO B0506+056 (05 09 25.9645434784 +05 41 35.333636817) z=0.3365 Outburst Type I Quasar S4 1800+44 (18 01 32.31481 +44 04 21.9004) z=0.663 Light curve. NASA's Fermi Gamma-ray Space Telescope Outburst Type ? 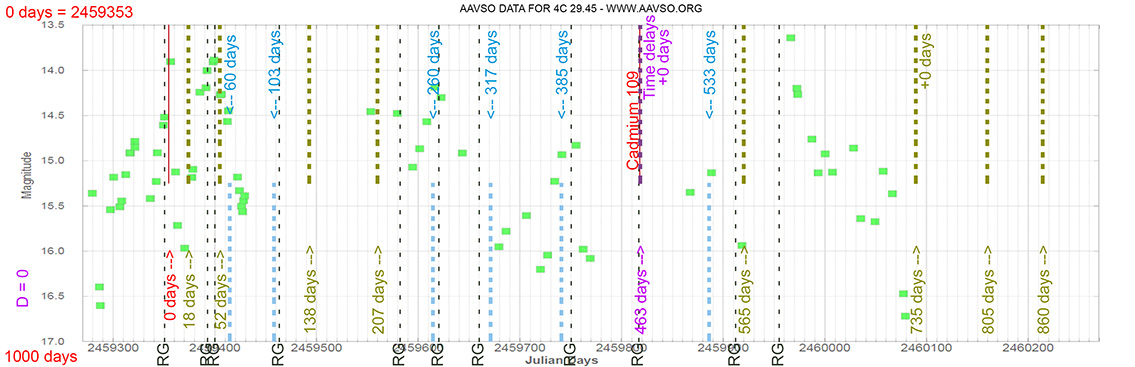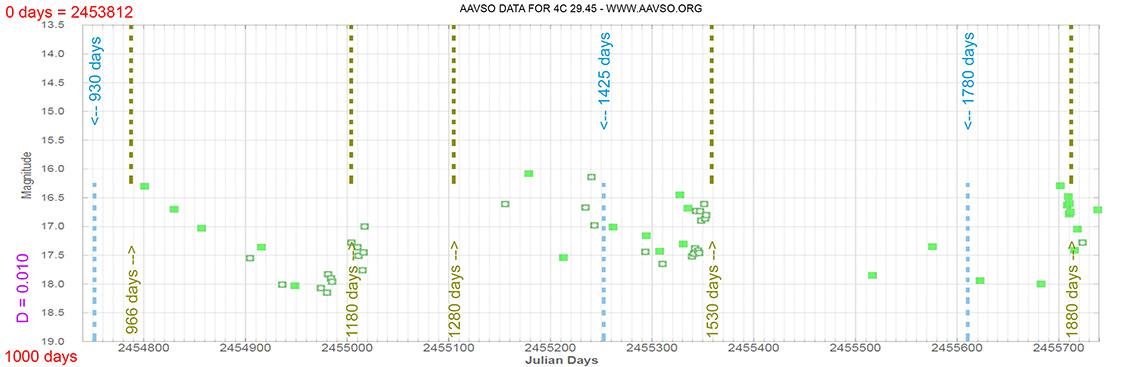Quasar 4C 29.45 (11 59 31.83390975 +29 14 43.8268741) z=0.72475 Outburst Type ? 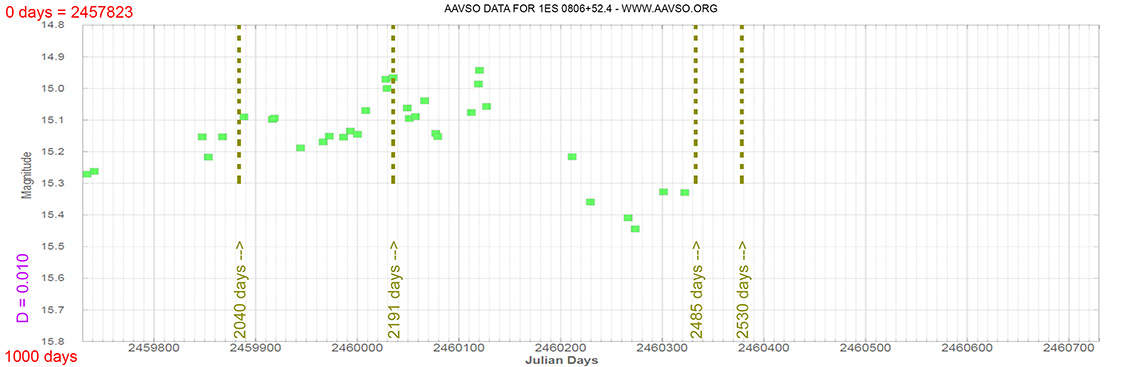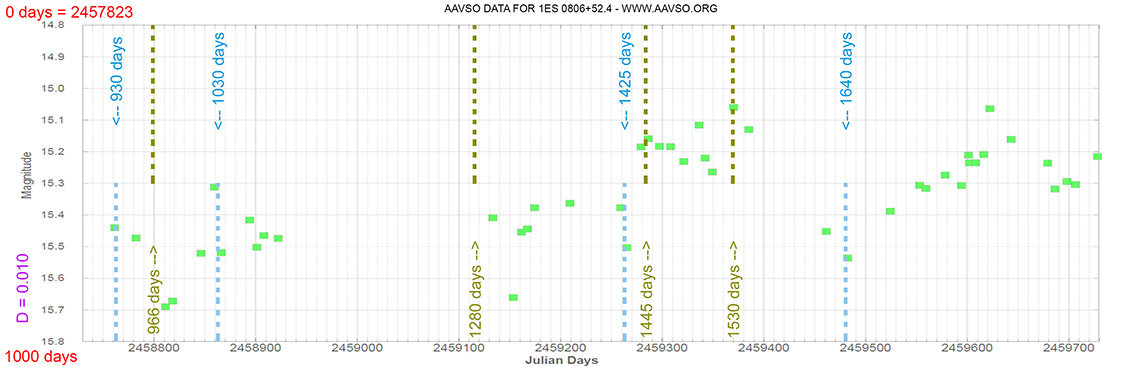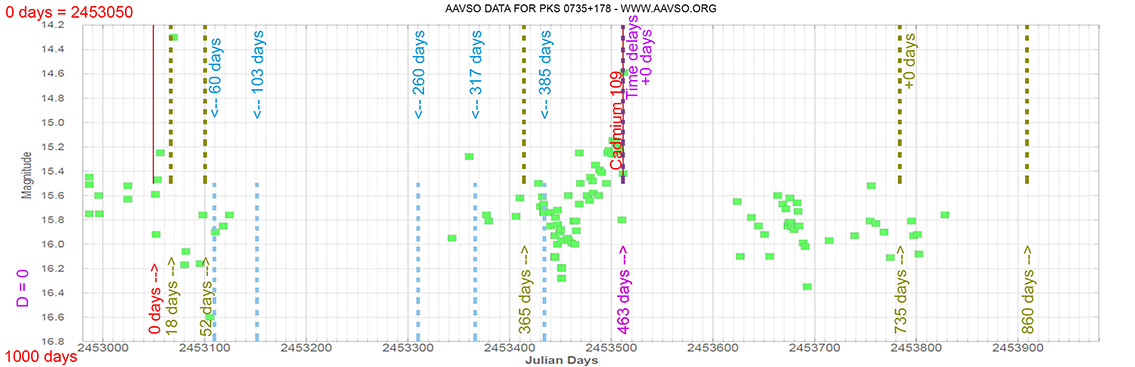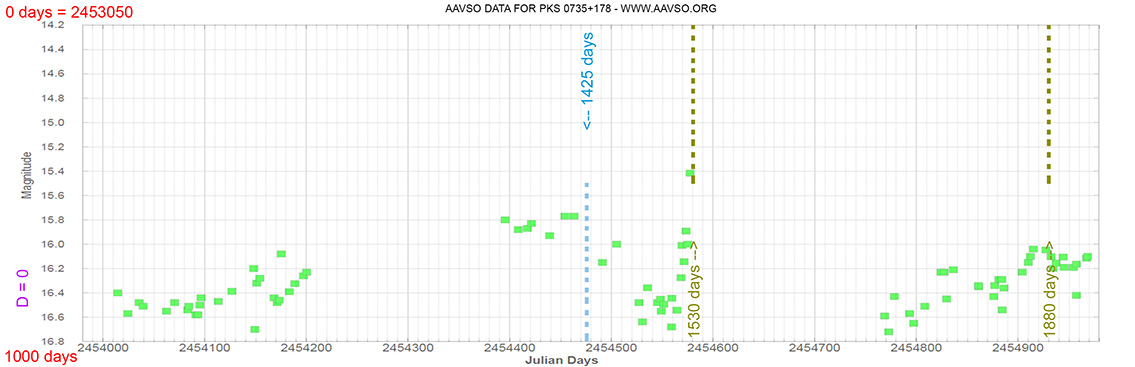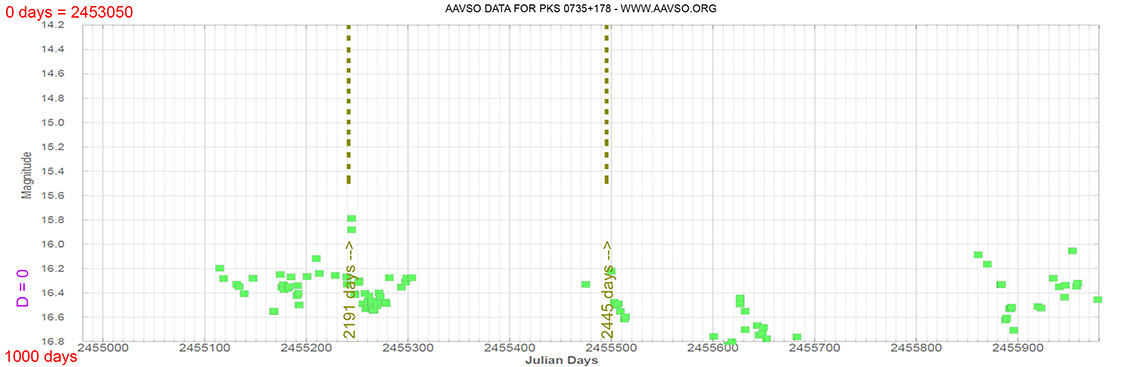Quasar 1ES 0806+52.4 (08 09 49.18673 +52 18 58.2507) z=0.13710 Outburst Type III Blazar PKS 0735+178 (07 38 07.39376 +17 42 18.9983) z=0.424 Outburst Type I Blazar QSO B1553+113 (15 55 43.0440 +11 11 24.366) z=0.360 Outburst Type ? 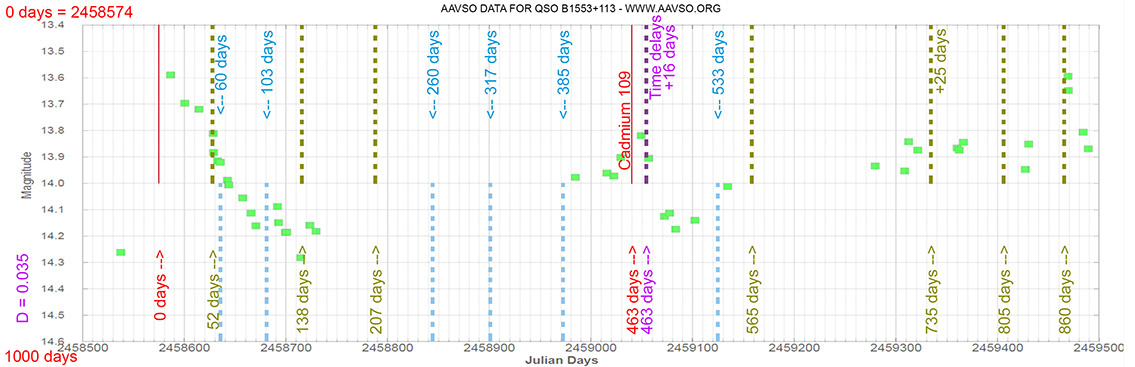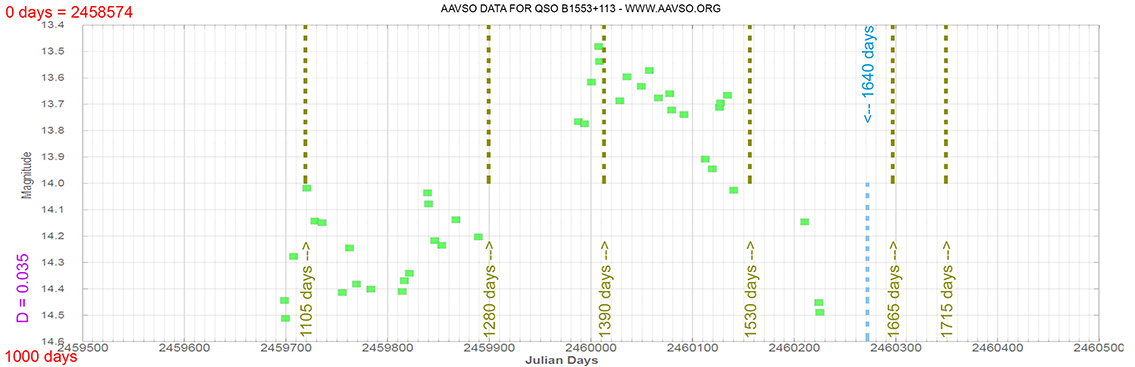Blazar NSV 19409 (12 30 14.0894 +25 18 07.136) z=0.135 Outburst Type ? 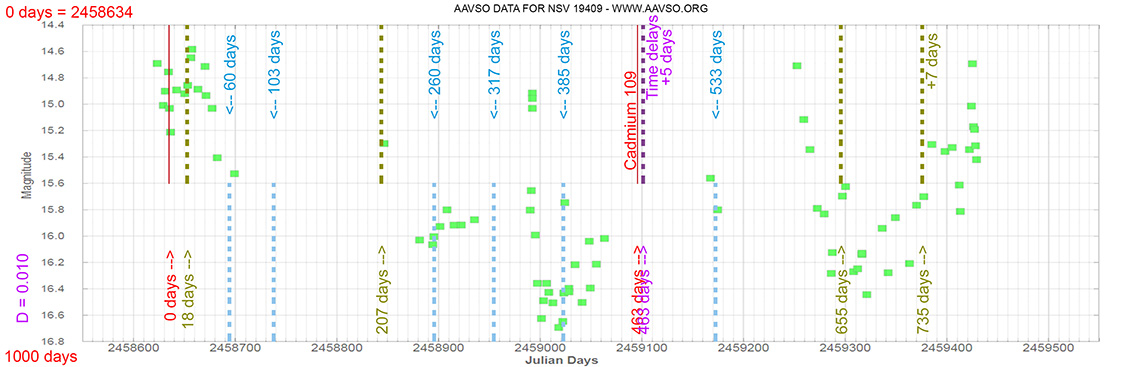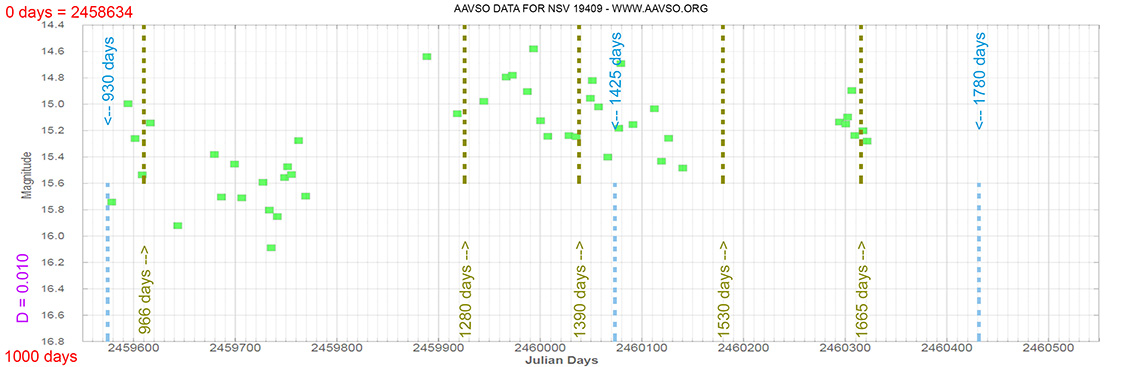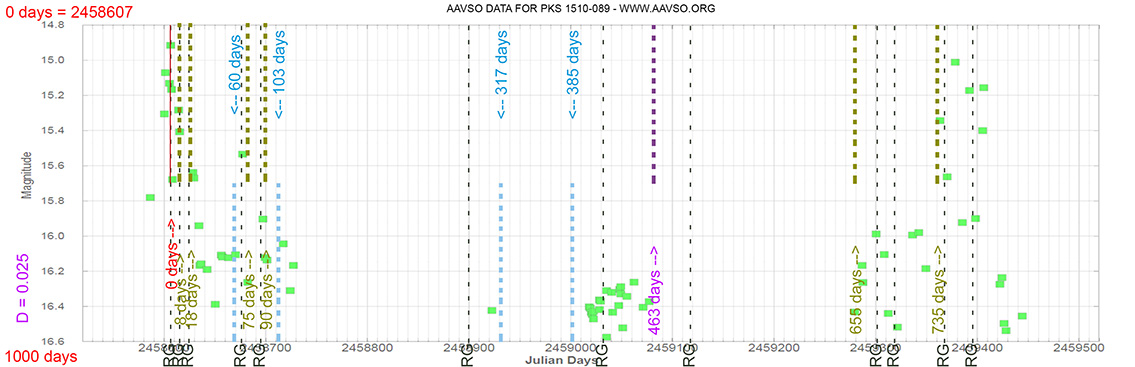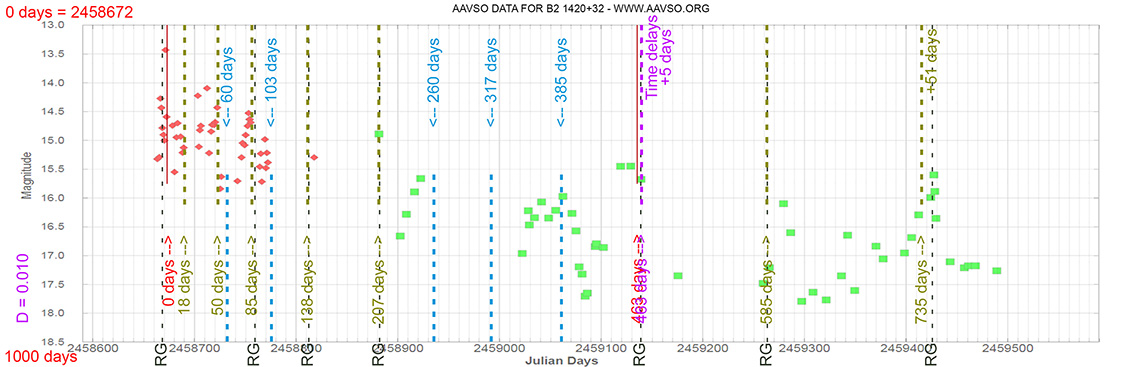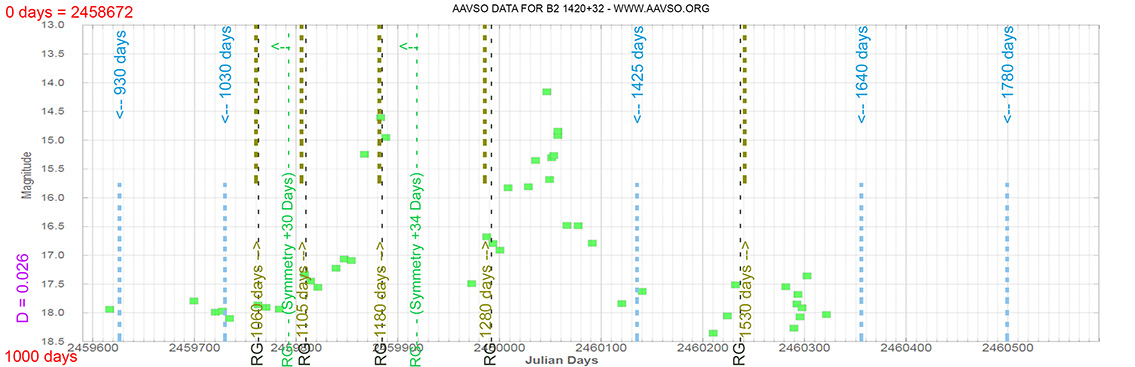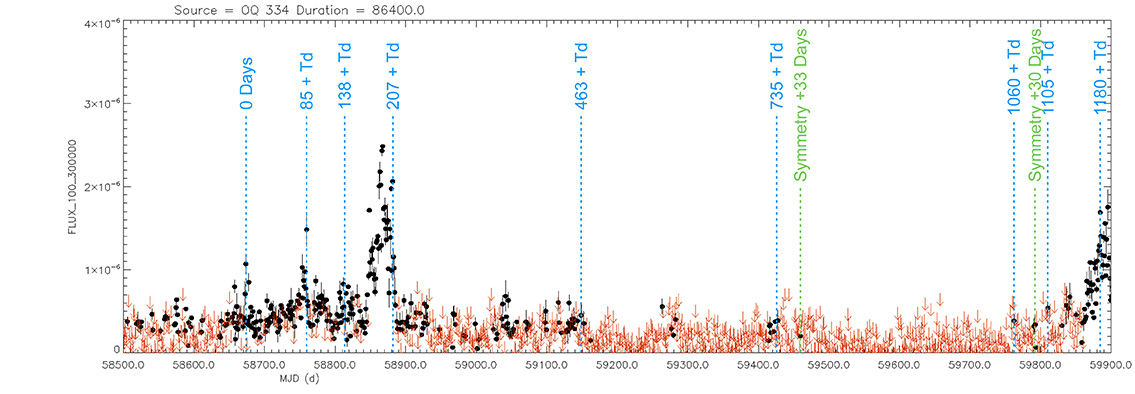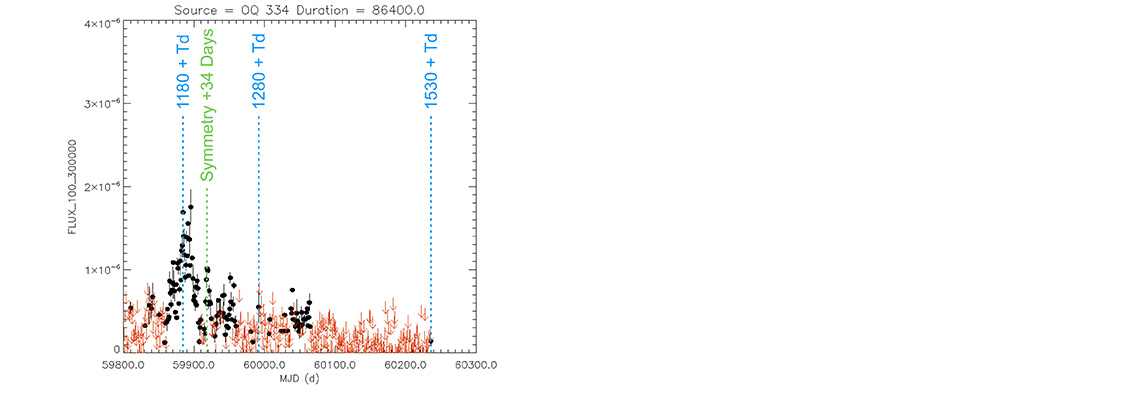Quasar PKS 1510-089 (15 12 50.53292 -09 05 59.8296) z=0.360 Outburst Type III Quasar B2 1420+32 (14 22 30.37890 +32 23 10.4446) z=0.68144 Light curve. 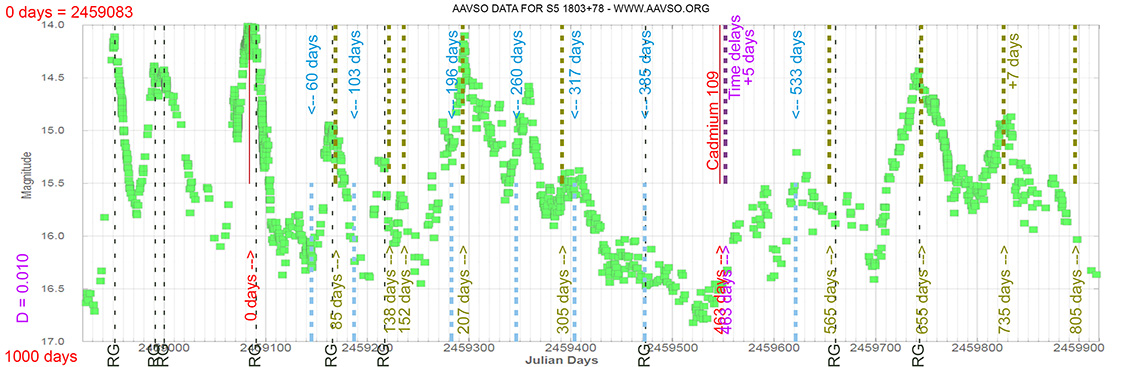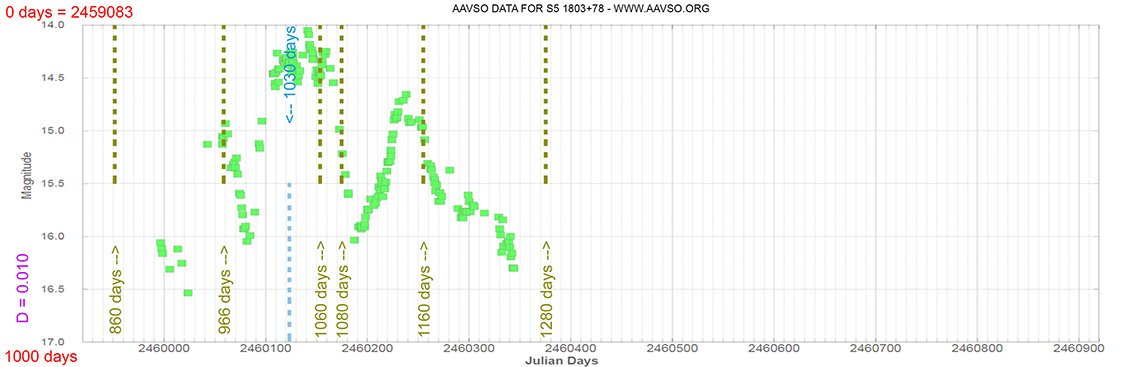NASA's Fermi Gamma-ray Space Telescope Outburst Type III Blazar S5 1803+78 (18 00 45.684 +78 28 04.02) z=0.680 Outburst Type III Blazar BL LAC (22 02 43.29139 +42 16 39.9803) z = 0.069 Outburst Type ?? 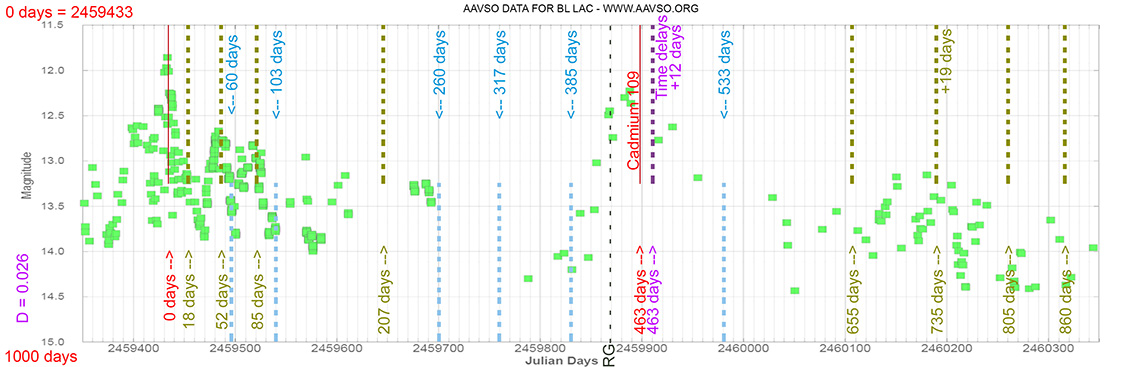Blazar S4 0954+65 (09 58 47.24510 +65 33 54.8181) z=0.367 Outburst Type ? 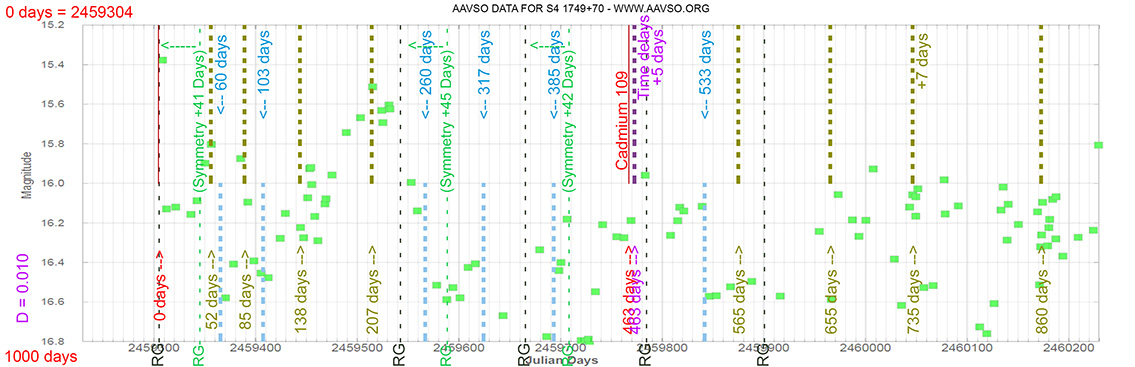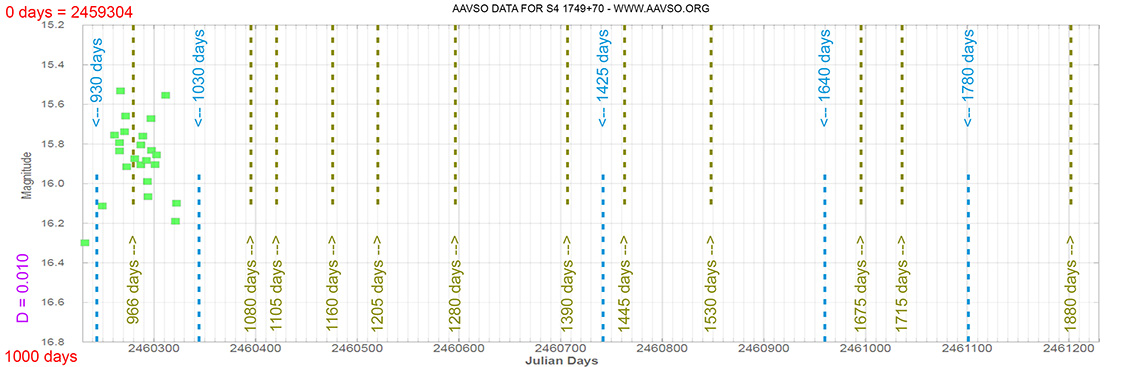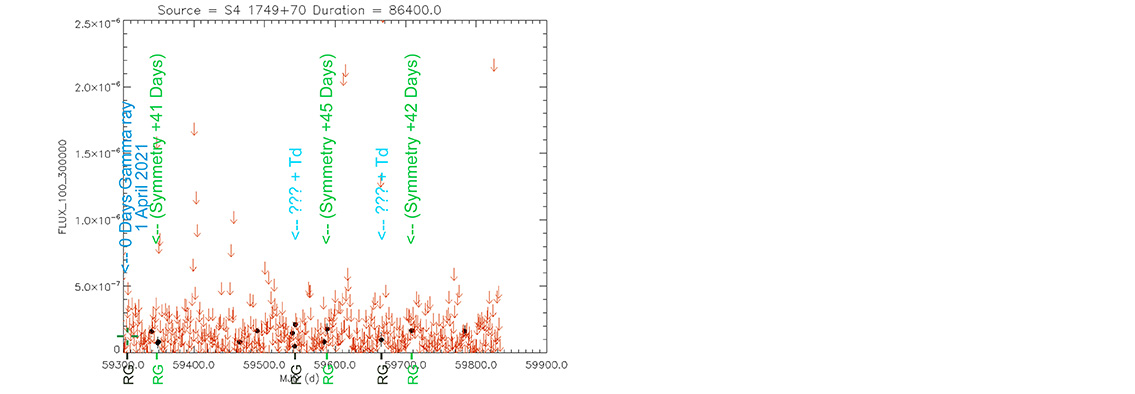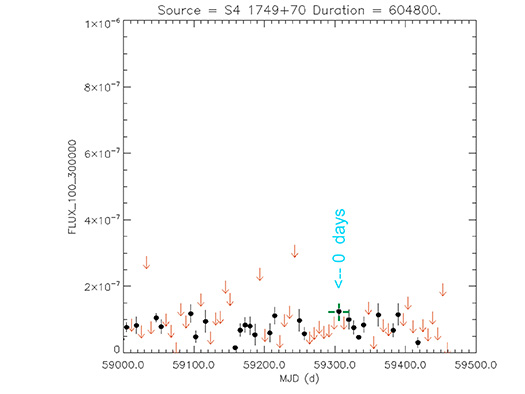Quasar 4C 29.45 (11 59 31.83390975 +29 14 43.8268741) z=0.72475 Outburst Type III Blazar S4 1749+70 (17 48 32.84043 +70 05 50.7684) z=0.770 Light curve. 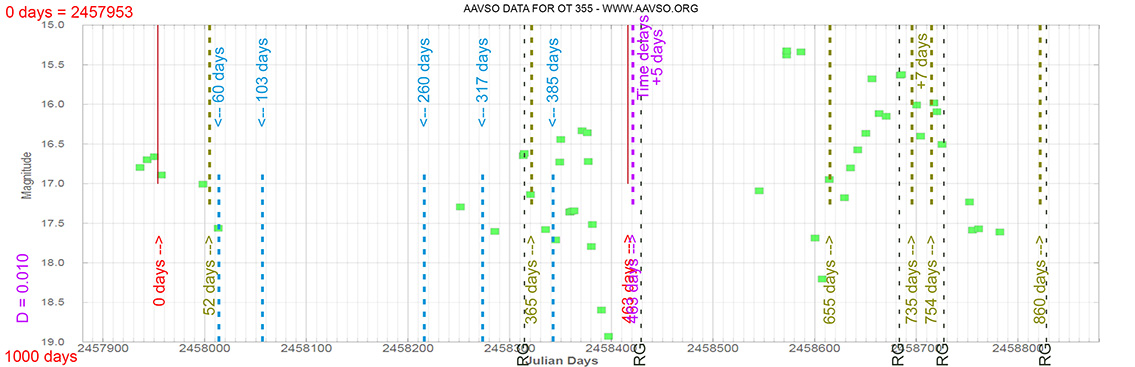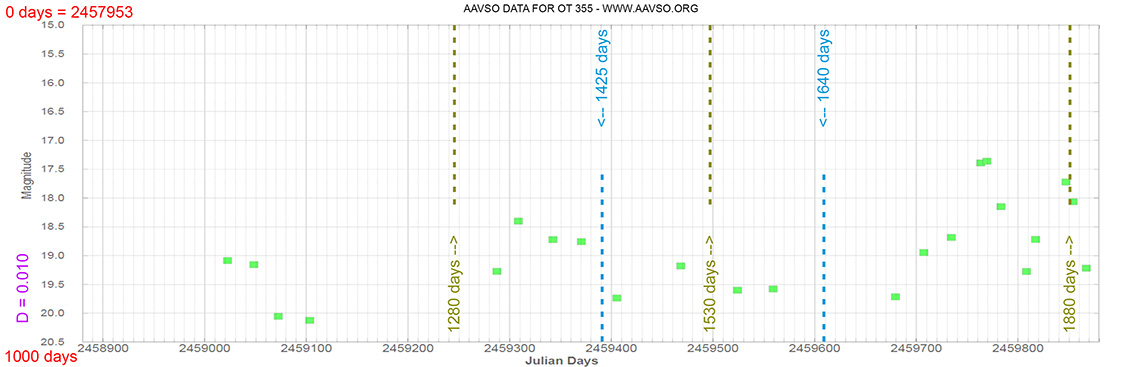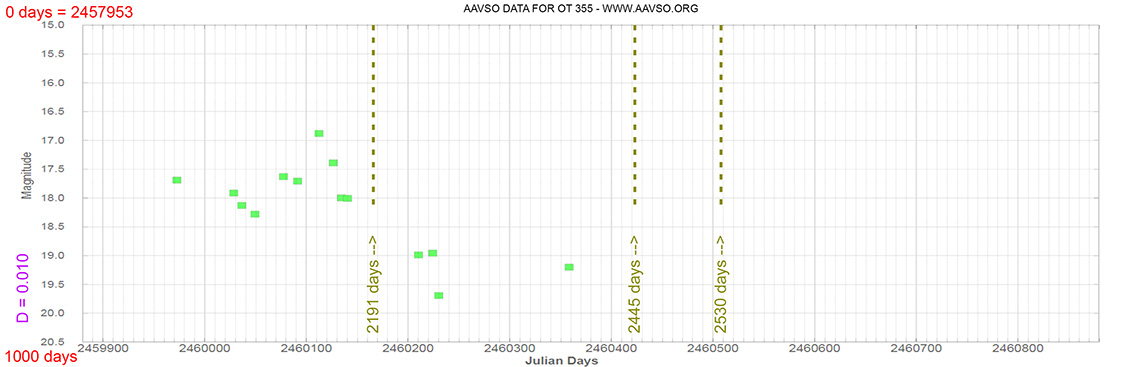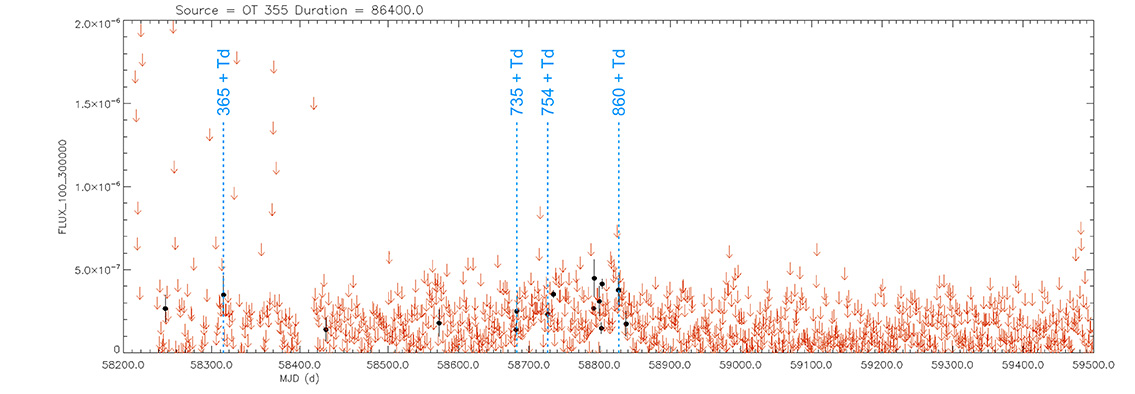NASA's Fermi Gamma-ray Space Telescope Explosión Tipo III Blazar OT 355 (17 34 20.57853650 +38 57 51.4430945) z=0.975 Light curve. 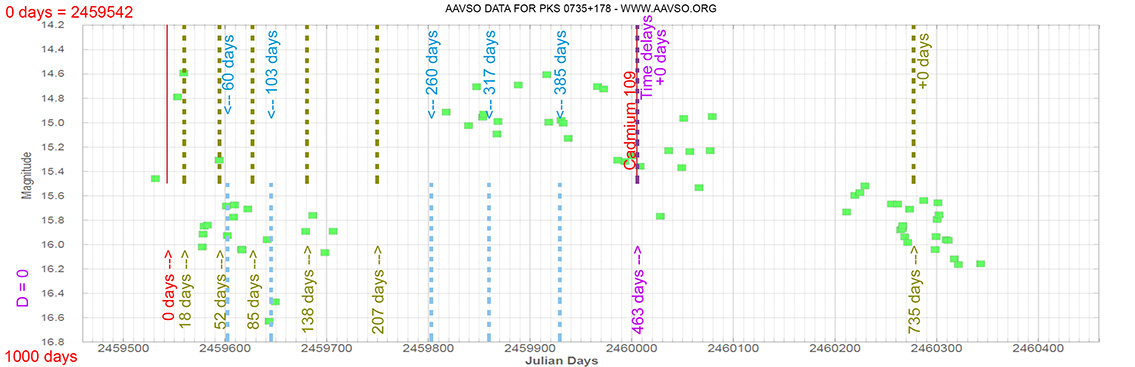NASA's Fermi Gamma-ray Space Telescope Outburst Type III Blazar PKS 0735+178 (07 38 07.39376 +17 42 18.9983) z=0.424 Outburst Type I Blazar B2 1147+24 (11 50 19.2122083392 +24 17 53.834712576) z=0.2090 Explosión Tipo III Blazar OJ 287 (11 50 19.2122083392 +24 17 53.834712576) z=0.2090 Explosión Tipo ? Blazar AU CVN (13 10 28.66385420 +32 20 43.7828340) z=0.99591 Explosión Tipo ?? Blazar 4C 31.03 (01 12 50.3328920232 +32 08 17.435303556) z=0.600 Conclusions - The Blazars have a temporary delay. This indicates that the observed light is very close to the event horizon of the black hole. - They have a recognizable pattern. They are predictable. - Secondary explosions correspond to radioactive decays and are in direct proportion to the intensity emitted. By comparing the intensity of these secondary explosions, we can know their amount of heavy elements. - All AGNs have their maximum and minimum periods, equal. This confirms that all AGNs are the same objects, viewed from different perspectives. - Although the maximum brightness at different wavelengths is related, there is a time delay of a few days with respect to other types of wavelengths detected, so that light emission does not occur exactly in the same place. Even in the main explosion, the maximum brightness in Gamma rays usually happens about 3 days earlier than in the optic. - The higher the frequency detected, for example, in Gamma rays with respect to optics, the faster its brightness can change. This indicates that the gamma-ray emitting region is much smaller than in the optical region. - By comparing the degree of time delay with other astrophysical magnitudes, we could discover related concepts. - Depending on the Blazar, the main explosion as secondary explosions may be more acute or flattened, in the curves of light. We could know why the cone of the emitting Jet is narrower than others. Gratefulness I thank the AAVSO for permission to publish their light curves and the M1 Group for their important contribution. Also to all observers who have made these observations, without them, this work would not have been possible. To all of them, thank you very much. Especially my partner Diego Rodríguez from the M1 Group. Gianpiero Locatelli, Ramón Naves, David Cejudo, Jose Luis Martin, Jordi Berenguer and Fernando Huet Grondona from the Supernova Group. Also Dave Hinzel and Heinz-Bernd Eggenstein from the AAVSO. And to Daniel Mendicini from the LIADA Group. Also the NASA Fermi Group to authorize publish their light curves in gamma rays for a greater understanding of these objects.